26a Si in parabola, vel hyperbola, linea ducatur penes diametrum sectionis: coincidet sectioni ad unum solum punctum.
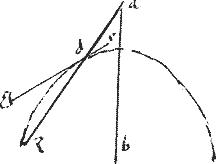
Sit prius parabole: cuius diameter abg322 recta autem ad et ducatur ez aequidistans ab323. // Aio quod ez324 producta coincidet sectioni. // Relinquatur enim quoddam325 punctum contingens326 in ez quod sit e. // Et ordinate ad diametrum ducatur eh. // Et sit ![]() dag maius, quam
dag maius, quam ![]() eh. // Et a puncto g ordinate ducatur gt.
eh. // Et a puncto g ordinate ducatur gt.
// Eritque per 11am327 huius ![]() [[ tg]]328 aequale
[[ tg]]328 aequale ![]() dag. // Quare
dag. // Quare ![]() tg maius quam
tg maius quam ![]() eh329. // Igitur tg maior quam eh cumque parallelogrammum sit ipsum eg iam ez producta secat ipsam tg. // Quare et sectioni coincidet // Coincidat ad [[ lc]] punctum330.
eh329. // Igitur tg maior quam eh cumque parallelogrammum sit ipsum eg iam ez producta secat ipsam tg. // Quare et sectioni coincidet // Coincidat ad [[ lc]] punctum330.
// Dico quod et ez sectioni ad solum c punctum coincidet. // Si enim possibile est: cadat et ad punctum l. // Igitur per 22am huius lc producta coincidet diametro ab331 quod est contra hypothesim. // Superest ergo ut ezc ad solum c punctum coincidat sectioni.
// Sit deinde sectio hyperbole, cuius quidem transversa diameter ab recta vero ad. // Et coniungatur bd et producatur eisdemque instructis, ducatur gm aequidistans ad332 rectae. // Quoniam igitur ![]() mga maius quam333
mga maius quam333 ![]() dag estque per 12am huius,
dag estque per 12am huius, ![]() mga aequale
mga aequale ![]() tg ideo et
tg ideo et ![]() tg maius quam
tg maius quam ![]() dag334. // Sed
dag334. // Sed ![]() dag per hypothesim, maius quam
dag per hypothesim, maius quam ![]() eh. // Igitur
eh. // Igitur ![]() tg maius, quam335 quadratum eh. // Quare et gt maior quam he. // Ergo sicut in parabola ez336 producta coincidet sectioni ad c punctum: et ad solum c punctum iisdem, quibus antea, repetitis: ac 22a huius citata. Quod demonstrandum fuerat337.
tg maius, quam335 quadratum eh. // Quare et gt maior quam he. // Ergo sicut in parabola ez336 producta coincidet sectioni ad c punctum: et ad solum c punctum iisdem, quibus antea, repetitis: ac 22a huius citata. Quod demonstrandum fuerat337.