F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Praeparatio ad Archimedis opera 44
<- App. -> <- = ->

PROPOSITIO XLIV.

In duobus circulis inaequalibus, id quod fit ex diametro maioris in peripheriam minoris, aequale est ei, quod fit ex diametro minoris in peripheriam maioris. Idemque de semidiametris, et semiperipheriis est dicendum.

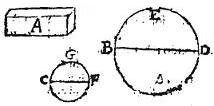
figura 29

Sunto duo circuli inaequales AGE, et BHF, quorum diametri AE, et BF, et peripheriae earum aequales sint lineis C, D, hoc est, ut per 15. huius, linea C sit aequalis peripheriae circuli AGE, et linea D aequalis peripheriae circuli BHF. Demonstrandum ergo est, quod rectangulum AED aequale est rectangulo BFC; nam cum per 8. huius, sicut est AE ad BF, sic sit C ad D; iam per 8. sexti Elementorum Euclidis constat prima propositi pars, quod si AI et BL supponantur semidiametri, iam per eandem 8. lineae C et D tunc erunt semiperipheriae. Unde constabit, quod supererat demonstrandum.

Inizio della pagina
 ->