F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Praeparatio ad Archimedis opera 45
<- App. -> <- = ->

PROPOSITIO XLV.

In tribus circulis, quorum diametri sunt in proportione continua, id quod fit ex diametro primi in peripheriam postremi, aequale est ei, quod fit ex diametro medii in peripheriam suam. Idemque de semidiametris, et semiperipheriis dicendum.

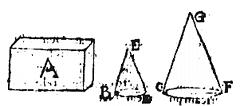
figura 30

Intersit enim per sextam huius, ipsis AG, et BL diametris media proportionalis linea EI, eritque per octavam huius, F peripheria circuli, cuius diameter EI, media proportionalis inter C, et D peripherias: quandoquidem peripheriae sunt diametris proportionales. Et demonstrandum erit, quod rectangulum AGD, sive rectangulum BLC (aequalia enim sunt per praecedentem) aequale est rectangulo EIF; nam cum AG ad EI sit sicut F ad D, iam per 15. sexti Euclidis constat prima propositi pars: et reliqua similiter; nam si AN, EO, et BR lineae supponantur semidiametri: erunt per 8. huius ipsae C, F, D, semiperipheriae. Constat ergo propositum.

Inizio della pagina
 ->