PROPOSITIO XLIII.

Circulus aequalis est ei, quod producitur ex semidiametro in semiperipheriam.

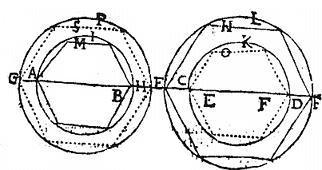
Sit circulus AGH, cuius semidiameter AB, superficies autem C sit id, quod fit ex semidiametro AB in semiperipheriam circuli AHG. Demonstrandum est, quod circulus AHG aequalis est superficiei C. Nam per 14. huius, erit circulus quispiam aequalis superficiei C; sit ergo circulus DIK cuius semidiameter BD aequalis superficiei C; et ostendendum erit, quod BD linea aequalis erit ipsi BA; nam secus, erit utravis maior, et circulus DIK describatur, concentricus circulo AGH, et per 12.12. Euclidis intra maiorem horum circulorum describatur figura multiangula, circulum minorem minime tangens, fietque per 1. sexti Euclidis ut superficies talis figurae inscriptae sit aequalis ei, quod fit ex aliqua linea inter ipsas AB, BD, quae sit BE, in ELM semiperimetrum ipsius figurae; quod productum sit F; itaque si AB sit maior, quam BD erit tunc BE minor, quam AB linea; et proinde superficies C maior superficie F; igitur tunc circulus DIK (qui aequalis figurae C positus fuit) maior erit figura F, seu ELM, quod est impossibile per tertium postulatum. Si autem AB sit minor, quam BD, tunc BE maior erit, quam AB linea; quare superficies F maior tunc est superficie C, et idcirco figura F seu ELM erit maior spatio C seu circulo DIK intra quem inscribitur:quod est impossibile per dictum postulatum. Cum ergo linea BD neque minor, neque maior possit esse, quam linea AB, erit aequalis. Quod erat demonstrandum.

Similiter autem ostendemus, quod superficies cylindrica aequalis est ei, quod fit [S:24] ex latere cylindrico in peripheriam basis. Idque per columnam inscriptam maiori cylindro, ita ut minorem non tangat. Item quod superficies conica aequalis est ei, quod fit ex latere conico in semiperipheriam basis. Idque per pyramidem inscriptam maiori cono, ita, ut minorem similem, vel sub eodem axe positum non tangat.