PROPOSITIO VIII

34 Aggregatum eorum quae fiunt ex utroque sinum duorum arcuum inaequalium in sinum secundum alterius rectangulorum ad differentiam eorundem est sicut sinus aggregati ex eisdem arcubus ad sinum arcus differentiae eorundem.

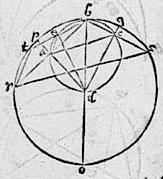
35 In circulo rbs cuius diameter bdo, centrum d, sint duo arcus inaequales pb bq quorum maior pb ductisque semidiametris dp dq. Ducantur¹⁶ ad ipsas dp dq lineae perpendiculares ba bc, quae productaeoccurrant periferiae apud rs eruntque dupli arcus bpr bqs¹⁷ ipsorum arcuum bp bq. 36 Ponatur item arcus bt aequalis arcui bs et ducatur chorda bt ad quam perpendicularis sit de et coniungantur lineae ac rs ae rt. 37 Quibus pactis, constabit ex diffinitionibus et ex prima praecedentis libri, quod sinus arcus bp est linea ba, sinus arcus bq est linea bc vel linea be quandoquidem earum duplae tb bs sunt [S:54v] aequales. 38 Item quoniam arcus rbs duplus est arcus ipsius pbq et ipsius rbs arcus chorda est rs, ipsius autem rs dimidium est ipsa ac iam ideo, per diffinitionem sinus ipsius arcus pbq erit linea ac. 39 Demum quoniam arcuum pb bq dupli sunt arcus rb bt et ipsorum arcuum rb bt differentia est arcus tr, iam ipse arcus tr duplus erit differentiae arcuum pb bq, sed ae linea dimidia est chordae tr igitur per diffinitionem linea ae sinus erit arcus qui differentia est arcuum pb bq. 40 Rursum ex prima praecedentis libri, sinus secundus arcus pb erit linea da, sinus autem secundus arcus bq erit linea cd vel linea de quandoquidem aequales sunt. 41 Itaque demonstrandum est quod aggregatum ex duobus quadrangulis quorum alterum sit ex ab cd, alterum vero ex bc da ad differentiam eorundem est sicut linea ac ad lineam ae. 42 Describatur super diametrum bd circulus, qui iam ibit per ipsa puncta a e c quandoquidem recti sunt anguli bad bed bcd. 43 Sic enim rectae ab bc erunt chordae arcuum inaequalium in tali circulo atque rectae be bc chordae aequales arcuum aequalium, recta ac chorda totius arcus abc aggregati scilicet ex arcubus ab bc, recta ae chorda differentiae eorundem, rectae ad dc chordae residuorum de semicirculo eorundem arcuum. 44 Quam ob rem per praecedentem, aggregatum quadrangulorum ab cd et quadrangulorum bc da ad differentiam eorum est sicut chorda ac ad chordam ae. Quod erat demonstrandum.