PROPOSITIO XV
101 In triangulo ex arcubus circulorum maiorum rectangulo in superficie [S:56r]sphaerae aggregatum ex sinu toto sinuque secundo anguli acuti ad differentiam eorundem est sicut quadratum quod ex sinu secundo dimidii anguli acuti ad quadratum quod ex sinu eiusdem dimidii.
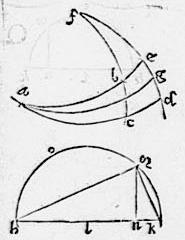
102 In descriptione 10 huius, arcus circuli magni ag secet per aequalia angulum bac: demonstrandum est iam quod aggregatum ex sinu toto, arcus scilicet df et ex sinu fe ad differentiam eorundem est sicut quadratum sinus arcus fg ad quadratum sinus arcus gd, hoc modo. 103 Exponatur sphaerae diameter hk, qua per medium secta apud l super eam, centroque l semicirculus describatur hmk. Ponaturque arcus mk aequalis arcui de ductisque chordis hm mk atque perpendiculari mn. 104 Erit iam hn linea congeries congeries sinuum arcus df arcusque fe, et linea nk differentia eorundem sinuum. 105 Sed per 17m sexti Euclidis, linea hn ad lineam nk est iam sicut quadratum lineae hn ad quadratum lineae mn et ideo propter similitudinem triangulorum, sicut quadratum lineae hm ad quadratum lineae mk. 106 Sed quadratum hm ad quadratum mk sicut quadratum sinus arcus fg ad quadratum sinus arcus gd (quandoquidem linea hm ad lineam mk sicut sinus arcus fg ad sinum arcus gd cum duplae sint lineae sinuum singulae singulorum). 107 Igitur et sicut quadratum sinus arcus fg ad sinum arcus gd sic linea hn ad lineam nk, hoc est sic aggregatum ex sinibus arcuum df fe ad differentiam eorumdem. Et hoc erat demonstrandum.