PROPOSITIO XXXIII

198 Si duo circuli maiores in superficie sphaerae angulum acutum contineant et in uno eorum signentur duo puncta a quibus arcus circulorum maiorum perpendiculares ad reliquum ducantur: ratio sinus arcus inter casus perpendicularium ad sinum arcus inter puncta signata cadentis componetur ex duabus, quarum una est ratio sinus totius ad sinum secundum unius arcuum perpendicularium, altera est ratio sinus secundi acuto angulo praedicto debiti ad sinum secundum reliqui arcus perpendicularis.

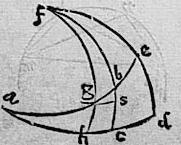
199 In superficie sphaerae duo circuli maiores ab ac angulum bac acutum contineant. Positisque quadrantibus acd abe ductisque, sicut in 17^a huius, circulorum maior quadrantibus def cbf hgf per puncta signata b g. Erunt iam bc gh arcus perpendiculares ad circulum ad, casus autem perpendicularium puncta c h. Sinus arcuum fb fg sinus secundi arcuum perpendicularium bc gh sinus arcus fe sinus secundus arcus de hoc est anguli acuti bac. 200 Itaque demonstrandum est quod: ratio sinus arcus hc ad sinum arcus bg componitur ex duabus, quarum una est ratio sinus arcus hf hoc est sinus totius ad sinum arcus fg, altera est ratio sinus arcusfe ad sinum arcus fb hoc modo. 201 Ducatur a puncto g circuli maioris arcus gs perpendicularis ad arcum fc. Sic enim posito medio sinu arcus gs, ratio sinus arcus hc ad sinum arcus bg componetur ex ratione sinus arcus hc ad sinum arcus gs [S:50v] et ex ratione sinus arcus gs ad sinum arcus bg. 202 Sed per 6^m huius, sicut sinus arcus hc ad sinum arcus gs sic sinus arcus hf ad sinum arcus fg. Per 7^m autem, sicut sinus arcus gs ad sinum arcus bg sic sinus arcus fe ad sinum arcus fb. 203 Igitur et ratio eadem sinus arcus hc ad sinum arcus bg componetur ex ratione sinus arcus hf est sinus totius ad sinum arcus fg et ex ratione sinus arcus fe ad sinum arcus fb. Quod fuit demonstrandum.