PROPOSITIONES I

11 Linea perpendicularis a puncto quopiam in periferia semicirculi ad diametrum est sinus rectus utriusque arcuum ab ipso puncto ad diametrum receptorum. 12 Portiones vero diametri a perpendiculari ad periferiam utrinque susceptae sunt sinus versi arcuum sibi singuli conterminorum. 13 Quae porro cadit inter perpendicularem et centrum est sinus secundus utriusque dictorum arcuum.

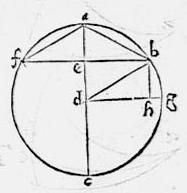
14 Circulus esto abc, cuius centrum d diameter adc; a puncto autem quolibet in periferia semicirculi abc utpote a puncto b ducatur ad adc diametrum perpendicularis [S:46r] linea be: dico iam quod be est sinus rectus tam arcus ab quam arcus bc. 15 Producatur enim be donec coincidat periferiae ad punctum f. Eruntque per 3^m tertii Euclidis be ef aequales, et per 4^m primi chordae ab af aequales et ideo per 28^m tertii, arcus ab af aequales. Quare arcus bc cf aequales. 16 Itaque cum be sit dimidium ipsius bf quae est chorda ipsius baf arcus dupli ad arcum ab iam per diffinitionem: erit sinus rectus arcus ab et per eadem, idem erit et sinus rectus arcus bc. 17 Excitetur ad rectos ipsi ac linea dg semidiameter et ipsi dg perpendicularis bh. Eritque, per dudum ostensa, sinus rectus arcus bg ipsa bh sed bg arcus complementum est arcus ab ad quadrantem, cum quadrans sit ag propter angulum rectum adg. 18 Igitur per diffinitionem, linea bh et ipsi aequalis ed erit sinus secundus tam arcus ab quam arcus bc. 19 Porro portiones ae ec erunt sinus versi arcuum ab bc singuli singulorum sibi conterminorum. Ex quibus ae est excessus semidiametri ad super ed sinum secundum ipsius arcus ab. 20 Ipsa vero ec est aggregatum ex semidiametro cd et ex linea ed sinu secundo arcus bc. Quemadmodum ex diffinitione constat. 21 Demum semidiameter dg est sinus tam quadrantis ag quam quadrantis gc, qui sinus totus sive maximus dicitur. 22 Praeterea coniuncta bd semidiametro, factus angulus bda subtenditur ab arcu ab supra quem constitutus est et ideo quicunque sinus fuit arcus ab idem et sinus erit anguli bde quem arcus ab subtendit, per diffinitionem. Et haec quo ad declarationem diffinitionum.