PROPOSITIO XXVII

163 Iisdem suppositis, si alternae quadrantum portiones sint aequales vel si arcus ipsius trianguli praedicti coniuncti quadrantem conficiant: tunc sinus secundus arcus reliqui erit medius proportionalis inter sinum totum sinumque secundum anguli oppositi et etiam aequalis sinui reliqui anguli acuti.

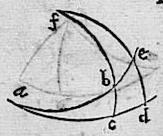
164 In eadem descriptione ponatur arcus ab aequalis arcui cd et ideo arcus ac aequalis arcui be vel, quod idem est, ponatur congeries arcuum ba ac quadrantes: aio tunc quod sinus arcus fb erit medius proportionalis inter sinum totum sinumque arcus fe et etiam aequalis sinui anguli abc. 165 Nam cum aequales ponantur coalterni arcus, erit sinus arcus ba ad sinum arcus ac sic sinus arcus cd ad sinum arcus be. Per 6^mautem huius, sicut sinus arcus cd ad sinum arcus be sic sinus totus ad sinum arcus fb. Et per 7^m, sicut sinus arcus ba ad sinum arcus ac sic sinus arcus bf ad sinum arcus fe. 166 Igitur sicut sinus totus ad sinum arcus fb [ad³³]sic sinus arcus bf ad sinum arcus fe. Itaque medius proportionalis est sinus arcus bf inter sinum totum sinumque arcus fe, quarum per 25^m huius, idem sinus arcus bf aequalis erit sinui anguli abc. Quae quidem proponebantur demonstranda.