PROPOSITIO XXV²⁸

151 Si trianguli rectanguli ex arcubus circulorum maiorum in superficie sphaerae et quadrantibus minorum, sinus secundus unius arcuum acutis oppositorum fuerit medius proportionalis inter sinum totum sinumque secundum acuti anguli oppositi: tunc reliqui arcus erunt altero complemento alterius aequales et sinus secundus praedicti arcus acutum subtendentis aequalis erit sinui reliqui acuti anguli.

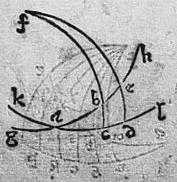
152 Sit triangulum sphaerale abc²⁹cuius latera quadrantibus minora, angulus autem c rectus. Et completis quadrantibus abe acd def cbf sicut in 17^a huius. Supponatur sinus arcus fb (qui est sinus secundus arcus bc) medius proportionalis inter sinum arcus cf, hoc est inter sinum totum et sinum arcus fe (qui est sinus secundus arcus ed <)³⁰>, hoc est anguli bac: aio tunc quod arcus ab aequalis erit arcui cd, et arcus ac aequalis arcui be itemque sinus arcus fb aequalis erit sinui anguli abc. 153 Nam per 6^m huius et permutatam proportionem, erit sinus arcus cd ad sinum arcus be sicut sinus totus cf arcus ad sinum arcus fb. Sinus autem arcus cf totus ad sinum arcus fb per hypothesim, sicut sinus arcus bf ad sinum arcus fe. Sinus etiam arcus bf ad sinum arcus fe per 7^m huius, sicut sinus arcus ba ad sinum arcus ac. Igitur sinus arcus ba ad sinum arcus ac sicut sinus arcus cd ad sinum arcus be. 154 Ponatur ergo ba aequalis arcus ag, ipsi be aequalis arcus eh, ipsi ac aequalis arcus ak, ipsique cd aequalis arcui dl. 155 Eritque chorda arcus bg ad chordam arcus ck sicut chorda arcus cl ad chordam arcus bh. Quandoquidem chordae duplicatorum arcuum sunt duplae sinuum simplicis arcubus debitorum, per diffinitionem. Et dupla sunt dimidiis proportionalia. 156 Ductis igitur talibus chordis, nec non diametris sive chordis semicirculorum gbh kcl, erunt duo triangula rectilinea gbh kcl super aequas bases, diametros scilicet gh kl circulorum aequalium et habebunt angulos gbh kcl aequales, quoniam recti sunt anguli super semicirculos. 157 Et ipsa triangula aequalia erunt per 14^m sexti, quoniam reciproca sunt latera, quae circum aequales angulos. Itaque per praecedentem, talium triangulorum reliqua latera reliquis lateribus singula singulis aequalia erunt, hoc est chorda gb chordae cl, et chorda kc chordae bh aequalis erit: maior scilicet maiori et minor minori. Igitur et arcus gb arcui cl, et arcus kc arcui bh aequalis erit. 158 Quare et eorum dimidium aequales, hoc est arcus ab arcui cd et arcus ac arcui be aequalis erit. Quod est primum ex demonstrandis. 159 Quoniam autem per hypothesim, sicut sinus totus ad sinum arcus fb sic sinus arcus fb ad sinum arcus fe. Per 6^m autem huius, sicut sinus arcus fb ad sinum arcus fe sic sinus totus ad sinum anguli abc velut fbe, propterea erit sicut³¹ sinus totus ad sinum anguli abc sic sinus totus ad sinum arcus fb. Eandem igitur rationem habet sinus totus ad sinum arcus fb et ad sinum anguli abc, quare aequalis erit sinus anguli abc sinui arcus fb. Et hoc restabat.