PROPOSITIO XI

84 Si duo anguli trianguli cuiuspiam ex arcubus circulorum maiorum in superficie sphaerae fuerint duobus angulis trianguli alterius ex arcubus circulorum maiorum in eadem superficie, singuli singulis aequales: tunc sinus arcuum aequalibus angulis oppositorum proportionales erunt.

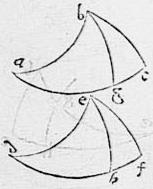
85 Sunto in superficie sphaerae duo triangula¹⁶ abc def ex arcubus circulorum maiorum, [S:47v] in quibus anguli a d sint aequales, itemque anguli bca efd aequales: aio quod sicut est sinus arcus ab ad sinum arcus de sic est sinus arcus bc ad sinum arcus ef. 86 Nam si tales anguli recti sint: arcus oppositi per 3^m huius, sunt quadrantes; atque ita constat propositum. 87 Si autem duo tantum ex angulis recti sint, ut qui ad c f, rursum per 7^m huius, constat propositum. 88 Si autem neutri recti fuerint, tunc a punctis b e perpendiculares arcus circulorum maiorum bg eh cadant ad arcus ac df si opus est productos. Cadent autem tales perpendiculares aut ambo intra triangula, aut ambo extra: propter aequalitatem angulorum ad bases. 89 Et quoniam aequales sunt anguli a d et qui ad g h recti, ideo iam per huius septimam, sicut sinus arcus ab ad sinum arcus bg sic sinus arcus de ad sinum arcus eh. Et per eadem et conversam proportionem, sicut sinus arcus bg ad sinum arcus bc sic sinus arcus eh ad sinum arcus ef. 90 Igitur ex aequali erit, sicut sinus arcus ab ad sinum arcus bc sic sinus arcus de ad sinum arcus ef. Et permutatim sicut sinus arcus ab ad sinum arcus de sic sinus arcus bc ad sinum arcus ef. Quod fuit demonstrandum.