THEOREMA XXXIV

114 Cavum speculum rei formam in oppositum planum ad terminum quendam proiicit inversam⁴²³.[C:24r]

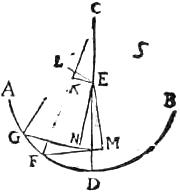
115 Cavum speculum AB rei CD formam recipiat per radios CE, CF⁴²⁴; DE et DF, et reflectantur⁴²⁵ CE et CF concurrentes ad signum G, at DE et DF ad signum H extra lineam EG, ut serventur⁴²⁶ aequi reflexionum anguli. Quoniam igitur possibile est, ut omnes radii a signo C ad speculum AB cadentes ad signum G fere⁴²⁷ concurrant⁴²⁸, a signo autem D ad signum H; et similiter a singulis rei CD partibus in speculum confluentes radii ad singulas partes impermixte⁴²⁹ concurrant, ideo⁴³⁰ in obiecto⁴³¹ plano in quo G, H et alia congressionum signa terminantur⁴³², forma rei CD conversa spectabitur⁴³³.

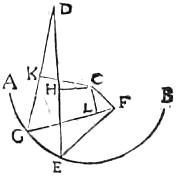
116 Item intelligantur in sphaera speculi duo maiores circuli ABCD et AECF, quorum communis sectio AC. Sitque res quaedam GH, cuius terminus G sit in semicirculo ABC, terminus autem H in semicirculo AEC. Si igitur terminus G in signum speculi C radiet, et signum H eodem, iam a signo G radius reflectetur ad semicirculum ADC, veluti ad punctum K, a⁴³⁴ signo vero H radius reflectetur ad semicirculum AFC, ut ad punctum L, quandoquidem in cavo speculo reflexio sit⁴³⁵ [S:29] in plano per centrum et ideo⁴³⁶ in plano circuli maioris, ut ex 27 satis liquet. Id enim planum ad sphaerici speculi superficiem rectum est. Ponatur autem puncta K, L, in quae[C:24v] a signis G, H in speculum cadentes radii concurrant, et similiter a singulis rei GH partibus in speculum perfluentes⁴³⁷ radii ad singulas concurrent partes, ita ut impermixte⁴³⁸ rei partes ad suam quamquam⁴³⁹ reflectantur partem. In plano igitur, in quo K, L⁴⁴⁰ et alia congressionum signa porrigentur, apparebit rei GH effigies conversa. In speculum ergo⁴⁴¹ quod parva est sphaerae portio, a signo quolibet ita perfluent⁴⁴² radii, ut omnes in unum fere signum reflexi concurrant.