THEOREMA XVI

43 Lucida sphaera in sphaeram se minorem radians ex ea plusquam hemisphaerium illustrat. Estque illuminatae superficiei terminus cir[C:9r]culus, et quae proiicitur umbra, conica est in vertice evanescens.

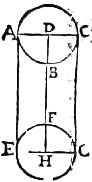
44 Lucida sphaera ABC¹⁰⁷, cuius centrum D, sphaeram se minorem irradiet EFG, cuius centrum H. Aio quod ex ea plusquam hemisphaerium illustrat; et illuminatae superficiei terminus est circulus; et umbra proiecta conica est. Secetur enim utraque ipsarum ABC et EFG sphaerarum¹⁰⁸ plano eodem per centra, sintque communes sectiones ABC et EFG circuli, et connectatur DH, periferiam ABC in signo B, et ipsam EFG in signo F secans. Et agatur radius AE, circulum ABC in signo A, circulum vero EFG in signo E contingens, et connectantur AD [S:11] et EH. Eruntque DAE et AEH anguli recti. Sed quoniam AD maior est ipsa EH, ideo acutus est angulus ADB. Concurrent ergo AE et DH ad partes EH. Concurrant itaque ad signum M, a quo ducatur MC recta ipsum ABC circulum contingens in signo C, quae necessario et ipsum EFG circulum continget.¹⁰⁹ Contingat ergo in signo G, et connectantur DC et HG. Et quoniam ABC arcus minor est semicirculo, maior autem EFG, ideo ducantur cordae, AC quidem ipsam DB secans in signo K, EG vero ipsam HM secans in signo L. Sit igitur MC radius ABC circulum atque adeo sphaeram ABC contingens in signo C, ipsum quoque EFG circulum in signo G, et ideo¹¹⁰ ipsam EFG sphaeram contingit. Sic omnes a signo M ad sphaeram ABC contingentes educti radii, ipsam quoque EFG sphaeram contingent. Et sicut in praemissa, ostendemus quod puncta contactuum in ipsa EFG sphaera sunt in circulo¹¹¹, cuius dimetiens est EG, centrum autem L. Quare hic circulus est terminus illuminatae superficiei. Et quoniam eius centrum extra sphaerae centrum est, ideo¹¹² minor est. Quare portio sphaerae EFG, in qua est centrum sphaerae, maior est hemisphaerio. Ergo portio sphaericae superficiei, cuius vertex F, illustrata, maior est hemisphaerio. Et quoniam radii contingentes omnes ad M signum concurrunt, ideo¹¹³ umbra quae proiicitur est conus, cuius basis est circulus dimetientem habens EG, vertex vero M. Quae fuerunt demonstranda.

Corollarium Primum¹¹⁴

45 Sphaera igitur a sphaera se maiore¹¹⁵ illuminata in planum cui perpendicularis est recta, quae sphaerarum centra connectit, circularem proiicit umbram;[C:10r] in planum vero, cui eadem obliqua est, umbram porrigit, quae sectio est conica. Patet, quoniam umbra quam sphaera a se maiori sphaera illustrata facit, conica est. Conus autem a plano, cui conicus axis perpendicularis est, sectus circulum in sectione facit; sectus vero plano cui¹¹⁶ axis obliquus est, conicam gignit sectionem. [S:12]

Corollarium Secundum

46 Hinc illud sequitur, ut sol, tam ex terra quam ex lunari globo, plus quam dimidium illuminet. Siquidem solaris sphaera et terrea et lunari maior est.

Scholium

47 Est notandum quod illud quod plus hemisphaerio illuminat sol, tam de lunari quam de terrestri corpore, in latitudine comprehendit tantum de¹¹⁷ ambitu corporis ipsius fere, quantum de periferia coeli¹¹⁸ continet semidiameter corporis solaris.