THEOREMA XV
40 Lucida sphaera in sibi aequalem sphaeram[C:8r] irradians, eius hemisphaerium illuminat umbramque proiicit cylindricam.

41 Lucida sphaera ABC, cuius centrum D, in sphaeram sibi aequalem EFG, cuius centrum H, irradiet. Aio quod eius hemisphaerium illuminabit, umbramque proiiciet cylindricam. Secetur enim utraque ipsarum ABC et EFG sphaerarum plano eodem per centra, sintque communes sectiones ABC, EFG circuli, et connectantur94 centra D, H et describantur dimetientes AC et EG ipsi DH orthogonales95, et connectantur AE et CG. Eritque AG parallelogrammum rectangulum, et ideo ipsae AE et CG erunt tam ABC quam EFG circulum contingentes. Quare et sphaeras ipsas ABC et EFG contingent. Similiter ostendemus quod omnes ipsarum ABC et EFG sphaerarum dimetientes ipsi DH orthogonales96 terminant puncta, in quibus extremi radii ipsas ABC et EFG sphaeras contingunt. Sed tales dimetientes per 5 XI in eodem sunt plano. Puncta igitur conta[S:10]ctuum in circulo sunt, cuius dimetiens AC in sphaera quidem ABC, in sphaera vero EFG sunt in circulo, cuius dimetiens EG. Hic97 igitur circulus terminus erit illuminatae superficiei. Et quoniam eius centrum est idem quod98 sphaerae centrum,[C:8v] ideo99 est circulus maximus in sphaera EFG.
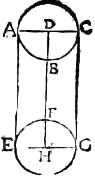
Unde sphaeram dividit in duo hemisphaeria. Hemisphaerium ergo100 est quod de sphaera EFG illuminabitur, cuius vertex F signum, in quo DH ipsam EFG periferiam secat. Et quoniam radii contingentes sunt101 latera cylindri, cuius bases sunt circuli, quorum dimetientes AC et EG, ideo tales radii ultra sphaeram EFG illuminatam producti umbram terminabunt cylindricam. Quod102 fuerat demonstrandum.
Corollarium
42 Sphaera igitur a sphaera sibi aequali illuminata in planum, cui perpendicularis est <recta103>, quae sphaerarum centra connectit, circularem104 porrigit umbram; in planum vero cui eadem est obliqua, umbram105 proiicit, quae cylindrica sectio est. Patet quoniam umbra106, quam sphaera a sibi aequali sphaera illuminata facit, cylindrica est. Cylindrus autem plano, cui cylindri axis perpendicularis est, sectus, circulum in sectione facit; sectus vero plano, cui axis obliquus est, cylindricam gignit sectionem.