THEOREMA XIV

35 Si lucidi signum sphaeram⁷¹ illuminet, minus quam hemisphaerium illustrat, et eo minus, quo sig[C:7r]num ad sphaeram propius accesserit, terminus autem illustratae superficiei⁷² semper circulus est.

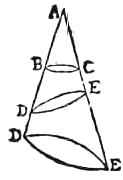
36 Sit lucidum signum A sphaeram BCD illustrans. Aio quod minus quam⁷³ hemisphaerium illustrat; et quo signum illustrans propinquius sphaerae fuerit, eo minor⁷⁴ erit illustratae superficiei portio; et quod terminus illustratae superficiei semper circulus est. Secetur enim sphaera BCD⁷⁵ plano per centrum et punctum⁷⁶ A, sitque communis sectio circulus BCD, cuius centrum E, et ducantur ab ipso A signo circulum BCD atque ideo⁷⁷ sphaeram contingentes lineae AB, AD et connectantur BD, ED, et EB, et AE periferiam BCD secans in signo C, ipsam autem BD in signo F. Quoniam igitur triangula orthogonia ABE et ADE invicem aequilatera sunt, erunt et aequiangula. Quare anguli⁷⁸ FAB et FAD invicem aequales. Unde fit ut ABF et ADF triangula sint aequilatera ad invicem, ideoque⁷⁹ aequiangula, et propterea qui ad F anguli recti. Aequalis ergo est BF ipsi FD. Similiter ostendemus quod a contactibus quorumlibet radiorum a signo A in sphaerae superficiem contingenter productorum⁸⁰ ad signum F ductae lineae sunt ad invicem aequales; et quod unicuique ipsarum perpendicularis est AF, et ideo⁸¹ per 5 XI omnes in uno iacere plano. Quare omnia contactuum signa in circulo esse, cuius [S:9] dimetiens⁸² [C:7v] BD ac centrum F. Igitur hic circulus terminus erit illuminatae superficiei. Et quoniam eius centrum F est praeter sphaerae centrum in linea EC, ideo erit minor. Unde portio sphaericae⁸³ superficiei lustrata, cuius vertex C, minus est hemisphaerio. Sit etiam aliud signum G in linea AE sphaerae propinquius. Iam ductis radiis contingentibus GH et GK, connexisque HK, in signo L ipsam EC secante, iisdem⁸⁴ nominibus patebit illustratae portionis terminum esse circulum, cuius dimetiens HK ac centrum L, et ipsius portionis verticem C signum atque ipsam HCK portionem ab ipso G signo illustratam minorem esse ipsa BCD ab ipso A signo illuminata⁸⁵.

Corollaria⁸⁶

37 1⁸⁷ Sphaera igitur a signo quopiam illuminata umbram proiicit non aliter quam⁸⁸ circulus a signo illuminatus.

38 2⁸⁹ Item quo propius fuerit signum illuminans sphaerae vel circulo, eo maiorem proiicit umbram.

39 3⁹⁰ Item tam a circulo quam a sphaera quae⁹¹ a signo quopiam illustratur, umbra progreditur semper crescens, similis coluro cono, quae quidem umbra solet a quibusdam calathoides⁹² appellari. Patent haec tria corollaria ex praemissis theorematis quam facillime⁹³.