Theorema X

Anguli¹⁰² inclinationum sunt fractionum angulis proportionales.

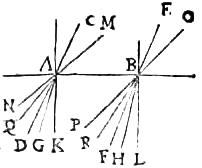
20 Ut si in plano diaphano ab, fuerint duo inclinati radii, cd¹⁰³ quidem ad signum g, at ef ad signum h fracti versus ipsas ak et bl perpendiculares, sicut primum vult suppositum, erit sicut angulus dak ad angulum fbl, sic angulus gad¹⁰⁴ ad angulum hbf¹⁰⁵. Fiant enim [A:3r] radii man et obp ad signa q et r fracti, ita ut ipsi nak et pbl anguli [C:30r] sint ipsorum dak et fbl angulorum utcumque multiplices. 21 Et tunc erunt per 3^um106 suppositum , ipsi¹⁰⁷ naq et pbr anguli¹⁰⁸ ipsorum dag et fbh angulorum similiter multiplices. Sed per 2^um109 suppositum, si angulus nak maior est angulo pbl, angulus quoque¹¹⁰ naq maior erit angulo pbr¹¹¹; et si minor, minor; et si aequalis, aequalis. Ergo per diff.¹¹² proportionalium [S:36] quantitatum, erit, sicut angulus dak ad angulum fbl, sic angulus dag¹¹³ ad angulum fbh, quod erat demonstrandum.

22 Corollarium

Ergo et angulus¹¹⁴ inclinationis ad angulum suae fractionis semper unam servat rationem. Sicut¹¹⁵ experimento in crystallina¹¹⁶ sphaera probavimus, estque dupla¹¹⁷ 2/3¹¹⁸ superpartiens¹¹⁹.

Unde¹²⁰, quoniam¹²¹ maximus inclinationis angulus est rectus, iam et angulus maximus fractionis in diaphanis habebit unius recti tres octavas.