<15>
59 Si in circulo triangulum aequilaterum descriptum fuerit: ipsius trianguli latus, potentia triplum est ad circuli semidiametrum.
Cir[S:114]culo abc triangulum aequilaterum abc sit inscriptum cuius circuli centrum d et diameter sit ade. Aio quod quadratum ipsius ab lateris triplum est ad quadratum ipsius ad vel de semidiameter.
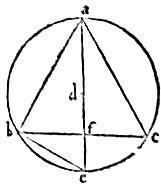
60 Connectatur enim be quod est latus hexagoni et ideo aequalis ipsi ad. Et hoc utere argumento. Nam quatuor quadrata ipsius ad sive be simul accepta, sunt aequalia quadrato ipsius ae diametri. Sed quadratum ae per penultimam Primi, aequum est quadratis ipsarum ab, be simul sumptis. Igitur quadrata haec simul sumpta, aequa sunt quatuor quadratis ipsius be. Quare dempto utrinque quadrato uno ipsius be supersunt tria quadrata be aequalia ipsi quadrato ipsius ab. 61 Triplum est ergo quadratum ipsius ab ad quadratum ipsius be sive ipsius ad quod fuit demonstrandum.
Unde manifestum est quod circuli diameter potest trianguli aequilateri et hexagoni aequilateri sibi inscriptorum latera.
Item patet, quod ab latus trianguli ad perpendicularem af potentialiter sesquitertium est. Et quod de semidiameter per aequalia secatur in puncto f.2
62 Quadrati quoque latus in circulo descripti potentialiter duplum esse ad semidiametrum circuli constat per sextam Quarti.
Descriptio autem pentagoni intra datum circulum fit per decimam et undecimam eiusdem.
Hexagoni vero latus aequum esse semidiameter circuli, conclusum est in quindecima eiusdem.
63 Ex his diviso per aequalia arcu lateris quadrati, notescit latus octogoni. Arcu quoque hexagonici lateris similiter secto, cognoscitur dodecagoni latus. Namque chorda dimidiati arcus est media proportionalis inter diametrum circuli et eius portionem, quae a chorda totalis arcus abscinditur.
Porro, si ponatur circuli diameter longitudine vel saltem potentia rationalis, latus octogoni intra circulum descripti, erit irrationalis linea, quae minor dicitur. 64 Latus vero dodecagoni linea irrationalis, quae apotome vocatur. Quod quidem ex ipso calculo constare potest: sicut et de lateribus pentagoni et decagoni in circulo rationalem diametrum habente descriptorum et de lateribus icosahedri et dodecahedri facere possemus.
Item pro calculo chordarum illud notandum, quod duae chordae semicirculum complentes, continent angulum rectum: unde una earum data, dabitur et reliqua per penultimam Primi. [S:115]
65 Et si quadrilaterum circulo inscriptum sit, tunc duo, quae producuntur ex binis oppositis lateribus, pariter accepta rectangula sunt aequalia ei, quod sub diametris eius comprehenditur, rectangulo, ut Ptolemaeus ostendit. Unde, si duorum arcuum datae sint chordae, dabitur tam eorum aggregati, quam differentiae chorda. Hinc arcuum per totum semicirculum chordae et sinus recti notescent. Et omnis chordimetria, quae tam ad planorum, quam ad sphaeralium triangulorum scientiam necessaria est. Nunc redeamus ad solida.