[A:10v] ELEMENTORUM QUARTUS

1 Figurarum inscriptiones et circumscriptiones sequuntur.

1^a

Intra datum circulum datam rectam collocare.

Oportet autem ut data non sit diametro maior.

2^a

Intra datum circulum constituere triangulum dato aequiangulum.

// 2 Duc tangentem et a contactu excita angulos duos. Trianguli duobus angulis aequales et argue per 31^am praemissi.

3^a

Circulo dato triangulum dato aequiangulum circumscribere.

// 3 Per praecedentem inscribe circulo triangulum dato aequiangulum. Mox duc tres parallelos lateribus trianguli circulum tangentes, quippe quae facient triangulum inscripto et perinde dato aequiangulum ac circulo dato circumscriptum.

4^a

Intra datum triangulum describere circulum. 4 Lineae dividant angulos singulos per aequalia, nam in puncto sectionis communis erit centrum.

5^a

Triangulo dato circulum circumscribere. Lineae dividant latera singula per aequalia orthogonaliter¹, nam in puncto sectionis earum erit centrum.

Corollarium

5 Unde patet quod in triangulo orthogonio circuli centrum cadit in medio lateris rectum angulum subtendentis. In oxygonio, intra. In amblygonio extra ambitum.

6^a

Intra datum circulum describere quadratum.

7^a

6 Circa propositum circulum describere quadratum.

8^a

Intra quadratum includere circulum.

9^a

Circa quadratum propositum describere circulum.

10^a

7 Isosceles triangulum construere, cuius anguli ad basim singuli duplum faciant anguli verticalis. Hoc opus, hic labor.

Exponatur ab recta, quae in puncto c per 11^am 2ⁱ secetur, ita ut rectangulum abc aequum sit quadrato ac.

8 Inde super centrum a lineetur circulus bd et recta bd per p^am huius ponatur ipsi ac aequalis. Et iungatur ad. [A:11r] Tunc enim triangulum abd erit quaesitum. Demonstratur hoc modo. Protrahatur dc et triangulo acd per 5^am huius, circumscribatur circulus acd quem recta bd tanget in puncto d per ultimam praemissi: quoniam rectangulum abc aequum fuit quadrato ac. 9 Quare, per 31^am praecedentis, angulus cdb aequalis est angulo bad.

Ergo angulus adb aequalis duobus angulis cdb, bad et perinde angulo bcd per 32^am pⁱ. Igitur angulus bcd aequalis angulo adb et perinde angulo abd. Quare per 6 pⁱ latus cd aequum lateri db et ideo lineae ca. 10 Ergo anguli cad, cda aequales fuitque angulus cdb aequalis angulo cad. Quam ob rem totus bda et ideo ipse abd angulus duplus est ad angulum dab /. Et tale triangulum proponitur faciendum.

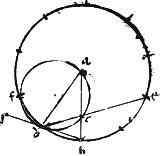
Scholium

11 Et quoniam, si per doctrinam 32^ae primi, recte calculum facias angulus bad habet duas quintas unius recti; concludes ergo² chordam bd esse latus decagoni aequilateri intra circulum dbe descripti. Item continuata dc usque ad periferiam ad punctum e concludes arcum be esse quintam partem periferiae totius. 12 Quoniam si angulus edb super talem arcum constitutus ad periferiam habet duas quintas unius recti, iam per 18^am praemissi, angulus super dictum arcum ad centrum, habebit quatuor quintas recti.

13 Item, quoniam angulus cad super arcum cd circuli parvi ad periferiam habet duas quintas unius recti: simili argumento ipse cd arcus erit quinta pars periferiae circuli parvi, et recta cd latus pentagoni in circulo parvo inscripti. Item³ arcus fd utriusque circuli aequant singuli ipsos arcus cd, db quoniam triangulum afd est aequilateris triangulo adb et ideo chorda fd aequalis chordae chordae db.

11^a

14 Intra datum circulum pentagonum aequilaterum inscribere.

Describatur, per 2^am huius, intra datum circulum triangulus qualem praemissa docet. Sectisque per aequalia, iis quae ad basim angulis, lineae secantes productae, cum angulis trianguli indicabunt in periferia, quinque puncta pentagoni quaesiti

12^a

15 Proposito circulo, pentagonum aequilaterum circumscribere.

Notatis per praemissam quinque punctis in periferia, quinque arcus aequos distinguentibus, per ea ducantur lineae circulum tangentes. [A:11v]

13^a

16 Intra pentagonum aequilaterum et aequiangulum, describere circulum.

Absolvitur, sicut quarta huius.

14^a

Pentagono aequilatero et aequiangulo circumscribere circulum.

Absolvitur, sicut quinta huius.

15^a

17 Circulo dato hexagonum aequilaterum inscribere.

Dato circulo, per 2^am inscribe triangulum aequilaterum, et divide singulos arcus⁴ per aequalia. Vel super semidiametrum colloca⁵ utrinque triangulum aequilaterum. Et continua in rectum tam semidiametrum, quam latera triangulorum per centrum. Sic enim tres diametri indicabunt 6 puncta angulorum hexagoni in periferia.

Corollarium

18 Hinc ostensum est, quod latus hexagoni aequilateri circulo inscripti aequum est circuli semidiametro.

16^a

Proposito circulo quindecagonum aequilaterum inscribere.

Per secundam cape trigonici lateris, per 11^am vero, pentagonici lateris arcum. Nam talium arcuum differentia habet duas quindecimas totius periferiae, quare eius dimidium erit quindecima, hoc est⁶ arcus lateris quindecagoni describendi. 19 Vel, si lubet, cape similiter arcuum pentagonicum et hexagonicum latera terminantium differentiam, quae iam erit pars 30^a totius differentiae et duplicata faciet quindecimam. Similiter differentia arcuum lateribus quadrati et hexagoni debitorum erit 12^a pars totius periferiae, et arcus dodecagonici lateris. At differentia arcuum quadrati et pentagoni erit arcus figurae 20^ti laterum. Et sic de reliquis.

Scholium

20 De caeteris autem figuris aequilateris, quae non dependent ab his, per differentiam, vel per divisionem arcuum, non datur regula.

Verum attende quod omnis figura aequilatera circulo inscripta est etiam aequiangula. Non autem e converso, nisi laterum numerus sit impar. 21 Item omnis figura aequiangula circulo circumscripta est etiam aequilatera: non autem e converso, nisi laterum numerus sit impar. Atque hic notandus est error Campani 4ⁱ libri finis.

4 februarii