[A:2r] EUCLIDIS ELEMENTORUM LIBER PRIMUS

1 Punctum est, cuius pars non est.

Linea, longitudo latitudinis expers.

Linearum alia recta, alia flexa.

Superficies, quae longitudinem et latitudinem habet.

Superficierum alia plana, alia curva.

2 Angulus est linearum concursus indirectus.

Angulorum, alius rectilineus, alius alteriusmodi.

Recta in rectam perpendicularis est, cum utrinque angulos facit aequales. Qui recti dicuntur.

Angulus recto maior, obtusus. Minor autem acutus.

3 Terminus est limes, seu finis.

Figura est, quae termino vel terminis clauditur.

Circulus est figura, cuius centrum a periferia aequaliter distat.

Hunc diameter per centrum in semicirculos dirimitur recta vero praeter centrum in portiones inaequales.

4 Rectilinearum figurarum quaedam sunt trilaterae, quaedam quadrilaterae, quaedam multilaterae.

Triangulorum rursus quoddam est aequilaterum. Quoddam isosceles. Quoddam vero scalenum. Aliud¹ orthogonium, aliud amblygonium, aliud oxygonium.

5 Quadrilaterarum, quaedam dicitur quadratum. Alia rhombus. Alia rectangulum. Alia rhomboides. Alia trapezion.

Rectae autem parallele sive² aequidistantes sunt, quae in eodem plano descriptae quorsumcunque et quantumcunque protractae contactum non admittunt. Limites³ et coincidentiae linearum sunt puncta.

Postulata

6 A puncto in punctum rectam describere, seu continuare.

Super datum punctum, ad datum spacium circulum designare.

Rectos angulos inter se esse aequales.

Duas rectas cum tertia complexas angulos duobus rectis minores concursum ire.

Duas rectas superficiem minime concludere. [A:2v]

Communes Sententiae

7 Uni et eidem aequalia esse invicem aequalia.

Aequalia adiecta congeries aequales: et subtracta reliquias aequales faciunt. Inaequalia vero inaequales.

Eiusdem tam dupla quam dimidia esse inter se aequalia.

Quae sibi invicem congruunt, invicem esse aequalia.

Totum parte maius esse. Et continens contento.

Scholium

8 Notandum quod tria ultima postulata verius reponi debent inter Communes Sententias. Sicut in graecis exemplaribus apparet. Sequimur hic traditionem Campani. Et possunt utrobique convenire quandoquidem tam postulata, quam communes sententiae sunt principia per se nota, et tanquam concessibilia supponuntur. Non tamen omnia Campani placita sunt admittenda. 9 Sicut nec Zamberti interpretis (qui Geometriam ignoravit) convitia sunt audienda. Rectius Faber ac modestius utrique viro consuluit, et studiosis omnibus profuit. Sed de his alibi latius.

Propositiones

p^a

10 Super datam rectam triangulum aequilaterum locare.

Super extrema datae, ad eundem spacium circuli describantur quorum bis coincidunt periferiae. Iungatur alterutra coincidentia cum extremis datae et factum erit.

[A:3r]

2^a

11 A dato puncto datae rectae aequalem rectam ducere.

Iungatur extremum datae cum puncto. Et super coniunctum triangulum aequilaterum locetur. Item super extremum ad spacium datae circulus describatur: et producto latere trianguli ad periferiam, super verticem trianguli ad spacium totius productae circulus lineetur: et reliquum crus trianguli ad huius circuli periferiam protendatur.

3^a

12 De longiori recta, breviori aequalem abscindere.

Coniungantur ad unum punctum: super quo ad spacium brevioris circulus describatur. Et factum est.

4^a

13 Duo triangula angulum angulo, et latera circum illos singula singulis aequalia invicem habentia: et basim basi et reliquos angulos reliquis singulos singulis aequales habet, et aequalia sunt.

Constat propositio: quoniam invicem congruunt.

5^a

14 Triangulum duorum aequalium laterum, habet angulos super et subter basim aequalis.

Patet per praecedentem: vel etiam per congruentiam repetitam. Unde triangulum aequilaterum est et aequiangulum⁴.

6^a

15 Triangulum duorum aequalium angulorum, habet et latera illis opposita invicem aequalia.

Secus enim sequeretur per antepraemissam, triangulum minus esse aequalem maiori. Hoc est partem⁵ toti. Unde triangulum aequiangulum est et aequilaterum⁶.

[A:3v]

7^a

16 Duas rectas duabus rectis conterminas, concurrentibus, ac singulas singulis aequales, eodem versus, alio concurrere est impossibile.

Impossibilitas sequitur per 4^am huius.

8^a

17 Duo triangula inter se aequilatera, sunt et aequiangula invicem et aequalia.

Congruunt enim. Secus sequitur impossibile per praecedentem. Unde astruitur propositum.

9^a

18 Datum angulum per aequalia dividere.

Super crura eius aequalia locetur triangulum aequilaterum: a cuius vertice ad datum angulum ducatur recta quae, per praemissam, datum angulum secabit per aequalia.

10^a

19 Datam rectam per aequalia dividere.

Super eam locetur triangulum aequilaterum, cuius angulus, per praemissam, secetur per aequalia. Nam recta secans angulum, secabit datam.

11^a

20 A puncto in data linea signato perpendicularem excitare.

Utrinque puncta aeque remota sumantur, et triangulum aequilaterum super interiectam locetur, cuius vertex cum puncto signato iungatur.

12^a

21 A puncto extra rectam, perpendicularem ad ipsam ducere.

Id vero fiet per circulum, qui rectam secet, et per divisionem anguli.

13^a

22 Recta rectae incidens, aut duos rectos, aut duobus rectis angulos aequales facit.

14^a

Si duae rectae a limite unius rectae exeuntes, contineant angulos aut rectos, aut duobus rectis aequales: unam faciunt rectam.

15^a

23 Rectae se invicem secantes, efficiunt angulos contra positos invicem aequales.

16^a

Extrinsecus angulus in triangulo maior est utrolibet intrinsecus sibi opposito.

17^a

Duo quilibet anguli in triangulo sunt duobus rectis minus.

18^a

24 Longius latus in triangulo opponitur angulo maiori.

19^a

Maior angulus in triangulo lateri longiori opponitur.

Ostenditur destructis contrariis.

20^a

Duo latera in triangulo simul sumpta excedunt reliquum.

Ex praemissa et collatione angulorum. [A:4r]

21^a

25 Duae rectae lateribus trianguli conterminae, intra triangulum coincidentes, breviores sunt, et maiorem angulum continent.

22^a

Ex tribus propositis lineis rectis triangulum construere.

Oportet autem ut duae simul sint reliqua maius.

23^a7

26 Ad terminum datae rectae angulum dato angulo aequalem constituere.

Ex praemissa fit.

24^a8

Si crura unius trianguli cruribus alterius trianguli singula singulis aequalia sint, angulus vero contentus angulo maior, tunc basis basi maior erit.

25^a

27 Quod si basis basim superet: et angulus angulum excedet.

Praecedens directae et praecedens a destructione contrariorum.

26^a

Duo triangula inter se aequiangula, et unum uni latus aequale sortita, et in totum sunt invicem aequilatera. Ex congruentia, et ab impossibili.

27^a

28 Rectae duae, super quas recta coalternos angulos facit aequales, parallelae sunt.

28^a

Item angulus extrinsecus intrinseco aequalis: aut duo intrinseci duobus rectis aequivalentes, easdem rectas parallelos faciunt.

Nam si concurrerent, triangulum haberet duos angulos aequales duobus rectis: quod est impossibile per 17.

29^a

29 Recta parallelis incidens facit angulos coalternos aequales extrinsecum⁹ intrinseco aequalem, duos intrinsecos duobus rectis aequales.

Conversa duarum praecedentium. Secus enim per quartum postulatum, concurrerent, quod esset contra hypothesim.

30^a

30 Duae rectae penes unam ductae, paralleli sunt.

Sequitur ex aequalitate angulorum per 27 vel 28.

31^a

Per punctum datum datae rectae parallelum construere.

Per angulum aequalem constitutum per 23 fit.

32^a

31 Extrinsecus angulus in triangulo duobus intrinsecis [A:4v] est aequalis, omnes autem tres anguli duobus rectis aequales.

Quod patet, ducta parallelo super angulum extrinsecum. Unde quadrilaterae figurae anguli quatuor rectos, pentagonae sex rectos, hexagonae octo rectos adaequabunt. Itaque deinceps. 32 Quod distincta figura in triangula constabit. Hinc in omni figura aequilatera et aequiangula, unius anguli quantitas per calculum notescet. Anguli autem cuiuslibet figurae extrinseci semper quatuor rectis aequivalebunt.

33^a

Parallelorum aequidistantium et aequalium¹⁰ extrema connectentes rectae sunt etiam aequales et paralleli.

Ex triangulis aequilateris ostenditur.

34^a

33 Parallelogrammum tam latera, quam angulos oppositos aequales habet. Et a diametro per aequalia dividitur.

// Id ex 26^a sequitur.

35^a, 36^a

Parallelogramma inter aequidistantes constituta lineas invicem aequalia sunt sive super eandem basim, sive super aequales.

37^a, 38^a

34 Id idem de triangulis concludimus.

Quandoquidem triangula ipsa sunt parallelogrammorum dimidia per 34^am.

39^a, 40^a

Quod si duo triangula super eandem sive super aequales bases locata sint aequalia; iam et inter aequidistantes lineas continebuntur.

Secus enim pars esset aequalis toti.

41^a

35 Parallelogrammum duplum est triangulo eiusdem basis ac celsitudinis.

Quoniam scilicet tale triangulum per 37^am aequale est triangulo, quod dimidium est parallelogrammi.

42^a

Triangulo proposito aequale parallelogrammum in dato angulo constituere.

Ex praemissa fiet.

43^a

36 Parallelogrammi supplementa parallelogramma circa diametrum invicem aequalia sunt.

Quoniam scilicet sunt [A:5r] excessus triangulorum aequalium.

44^a

37 Super datam rectam parallelogrammum proposito triangulo aequale in dato angulo constituere.

Ex praemissa fit et demonstratur. Hinc¹¹ et cuilibet rectilineo, super datam lineam et in dato angulo aequale constituetur parallelogrammum.

45^a

38 Ex data recta quadratum describere.

Utere doctrina 11^e ac 2^e.

46^a

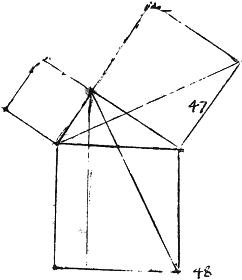
In triangulo rectangulo, quadratum maximi lateris aequivalet duobus quadratis reliquorum.

Ducatur perpendicularis ab angulo recto ad latus oppositum, et continuata secet quadratum ipsius in duo parallelogramma, quae quidem singula singulis quadratis minoribus, aequalia ostendentur et idcirco totum ambobus aequale. Id autem per triangula aequalia et dimidia eorum, quorum aequalitas concludere.

47^a

39 Quod si quadratum unius laterum trianguli aequum sit quadratis duobus reliquorum: iam et rectus erit illi oppositus angulus.

Constructo enim alio triangulo rectangulo cum cruribus aequalibus ad propositi trianguli crura concluditur id ex praemissa, sive per 8^am sive ab impossibili per 7^am huius primi.

48^a

40 Hinc fieri poterit duobus vel quotlibet propositis quadratis aequale quadratum.

Et propositorum quadratorum construere aequum quadratum.

Elementorum Primi finis

18 Ianuarii