[A:52r] Euclidis Elementorum liber secundus
<1> 1 Parallelogrammum rectangulum sub conterminis lateribus contineri dicitur.
<2> Partiale autem parallelogrammum, quod circa diametrum una cum supplementis sumptum gnomon vocetur.
1a
2 In quamvis lineam producta partium conficiunt productum integri.
| ||||||||||||||||||||||||||||||
Constat per se, sive per lineas, sive per numeros agas.
2a
3 Producta partium in totum conflant quadratum totius.
| ||||||||||||||||||||||||||||
3a
4 Quadratum partis cum producto partium consummat productum totius in dictam partem.
| ||||||||||||||||||||||||||
|
4a
5 Quadrata partium cum duplo producti partium constituunt quadratum totius.
| ||||||||||||||||||||||||||||||||||||||||
5a
6 Linea aequaliter et inaequaliter divisa, productum partium inaequalium cum quadrato mediae aequiperat quadratum dimidiae.
Per 4am, 3am, pam.1
| |||||||||||||||||||||
6a
7 Productum totius in adiectam cum quadrato dimidiae conficit quadratum ex aggregato dimidiae et adiectae.
Constat per 4am et pam.2
|
7a
8 Quadratum totius cum quadrato unius partium valet duplum producti totius in ductam partem cum quadrato reliquae partis accepti.
Per 4am et 3am.3
| |||||||||||||||||||||||||
8a
9 Item quadratum totius aequivalet quadruplum producti partium cum quadrato differentiae partium acceptum. Per 4am4.
| |||||||||||||||||||||||||||||
9a
10 Linea aequaliter et inaequaliter divisa, quadrata partium inaequalium conflant duplum quadratorum, quae ex dimidia et ex media.
Per 4am et 7am.5
| |||||||||||||||||||||||||
10a
11 Quadratum totius cum quadrato unius partis duplum efficiunt quadratorum quae fiunt ex dimidio reliquae partis et ex ea, quae constat ex tali dimidio et parte alia.
Per 4am et 7am6.
|
11a
12 Datam lineam sic secare, ut quod sub tota et una partium continetur, aequum fit quadrato reliquae.
ab sit linea data. Eius quadratum abcd. Ipsius ab 1/2 sit be. Ipsique ea aequalis ef et compleatur quadratum bfgh. Nam tunc ab in puncto h sic secatur, ut proponitur. [A:52v]

13 Nam cum db per aequalia secetur in puncto e.
|
per 6am valet |
Ergo per penultimam primi valent
14
Quare, dempto utrinque ![]() be superest
be superest ![]() df fb aequum
df fb aequum ![]() ab.
ab.
Et rursus, dempto utrinque ![]() lo dbh, superest
lo dbh, superest ![]() lum ch aequum
lum ch aequum ![]() hf.
hf.
Igitur linea ab in puncto h secta est sicut proponitur. Unde, si ponatur linea ab 4or pedum erit be 2 pedum. Quare linea ab ![]() 20 et ideo bf, hoc est bh erit
20 et ideo bf, hoc est bh erit ![]() 20
20 ![]() 2 irrationalis, quae vocatur Apotome quinta.
2 irrationalis, quae vocatur Apotome quinta.
12a
15 Cathetus intrinsecus in triangulo ita dividit basim, ut quod fit ex differentia portionum in totam basim, aequale fit differentiae quadratorum quae ex reliquis lateribus.
In triangulo abc cadat perpendicularis bd in basim ac sitque portio cd maior quam da cuia equale sit de eritque portionum basis differentia ec. Eritque

|
per 6am aequum |
16
Apponatur utrobique ![]() bd 11 eritque per penultimam primi
bd 11 eritque per penultimam primi
|
aequum |
Corollarium
17 Igitur differentia quadratorum ab, bc divisa in basim ac exhibet lineam ec, quae est differentia portionum.
13a
In omni triangulo latus oppositorum acuto coeteris duobus minus potest [A:53r] duplo producti unius eorum et portionis eius, quae perpendiculari et acuto interiacet.
18 Sic argue
| |||||||||||||
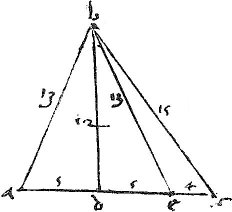
19
Igitur ![]() tum bc minus potest
tum bc minus potest ![]()
![]() tis ipsorum ab, ac simul sumpti in
tis ipsorum ab, ac simul sumpti in ![]() lo ac ea, hoc est in duplo
lo ac ea, hoc est in duplo ![]() ac ad quod est propositum. Et est propositio 13a 2i Euclidis.
ac ad quod est propositum. Et est propositio 13a 2i Euclidis.
14a
20 In triangulo amblygonio, latus obtusum subtendens angulum plus potest duobus caeteris duplo producti unius eorum et continuatae usque ad cathetum ab acuto cadentem.
Triangulum abc habeat angulum bac obtusum et ca producta occurrat perpendiculari bd apud punctum d. Et sic argunt.
|
per 4am |
21
Ergo apposito utrobique ![]() to bd, ex penultima primi
to bd, ex penultima primi
|
simul aequalia erunt |
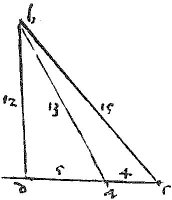
Quare ![]() tum bc lateris respicientis angulum bac obtusum maius potest lateribus ba, ca in duplo
tum bc lateris respicientis angulum bac obtusum maius potest lateribus ba, ca in duplo ![]() ca ad quod est propositum. Et haec est propositio 12a 2i Euclidis.
ca ad quod est propositum. Et haec est propositio 12a 2i Euclidis.
15a
22 Cathetus extra occurrens basi productae in triangulo amblygonio efficit differentiam quadratorum ex reliquis lateribus aequalem ei, quod fit ex basi, in eam quae constat ex ipsa basi duploque lineae sequentis usque ad cathetum.
Constat in figuratione 13ae praemissae.
Corollarium
23 Igitur in figuratione praecedentis differentia quadratorum ab, bc divisa per [A:53v] basim ac exhibet aggregatum ex ac duploque ad unde si a tali aggregato auferantur ac superest duplum ipsius ad cuius 1/2 erit ad.
16a
Dato parallelogrammo rectangulo aequale quadratum describere.
24
Sit datum rectangulum quod ex ab in bc. Secetur ac per aequali in puncto d. Et ![]() tum cd excedat
tum cd excedat ![]() tum db in
tum db in ![]() to lineae e. // Tunc enim per quintam,
to lineae e. // Tunc enim per quintam, ![]() tum lineae e erit aequum
tum lineae e erit aequum ![]() lo abc. Namque per 5am,
lo abc. Namque per 5am,
|
aequalia sunt |
25 Sed per hypothesim
|
aequalia sunt |
Igitur ablato utrinque ![]() to db, superest
to db, superest ![]() abc aequale
abc aequale ![]() to e quod erat faciendum.
to e quod erat faciendum.

17a
Dato triangulo aequum quadratum describere.
26 Constituatur parallelogrammum rectangulum aequale dato triangulo per 42am primi. Et per praecedentem, parallelogrammo aequum quadratum.
18a
Dato trapezio sive quotcunque laterum rectilineo, aequale quadratum describere.
27 Resolvatur trapezium sive rectilineum in triangula et triangulus singulis per praecedentem describantur quadrata singula aequalia deinde per penultimam primi, fiat quadratum omnibus illis quadratis aequale. Quod quidem aggregato triangulorum et perinde proposito rectilineo aequum erit. Sic per17 calculum notae sunt18 demonstrationes.
Hora 22a diei ![]() quae fuit dominica 60a 29o Ianuarii 1570
quae fuit dominica 60a 29o Ianuarii 1570