[A:26r] PTOLEMAICAE TRADITIONES,
EX SINGULIS MAGNAE CONSTRUCTIONIS LIBRIS
Ex Primo
1 Speculativa pars philosophiae cum in tria genera diuidatur secundum Aristotelem, naturalem scilicet, mathematicum ac theologicum. Cumque theologia sit supra facultatem humanam, et incomprehensibilis, physica vero, propter authorum discrepantia etmateriae fluxum incerta; commendatur mathematica et precipue astronomia propter certitudinem demonstrationis et subiecti nobilitatem.
2 Coeli figuram esse sphaericam, et motum eius circularem. Hoc enim triplici syllogismo concluditur, scilicet experientia, confutatione, ac ratione.
Terram esse rotundam. Rotunditas secundum longitudinem ex ortu et occasu stellarum, et ex eclipsi Lunae convincitur, et quod intervalla temporum proportionalia sunt interstitiis locorum. 3 Rotunditas autem ab austro ad boream ex apparitionibus perpetuis stellarum et ex altitudinibus earum meridianis, quippe quarum crementa proportionalia sunt latitudinibus climatum. Item aquae rotunditas ex apparitione successiva scopulorum arcium atque insularum.
4 Terram in medio mundi sitam esse. Secus enim nec semicirculos ex circulis maioribus, neque coeli hemisphaerium cerneriemus, neque aequinoctia, neque crementa dierum correlatiua, neque eclipsium lunarium ratio procederet. Item cum ex perpendiculis, et eclipsibus dictis conuincatur Terra esse in duabus1 diametris mundi, necessario sequitur ut sit in centro.[A:26v] 5 Terram respectu firmamenti puncti vicem habere. Secus enim non videremus coeli dimidium non stellas et astra semper eiusdem magnitudinis. Item distantia centrorum instrumenti et Terrae inferret sensibilem in observationibus diversitatem. Quod Terra localem motum non habet, ostendere. 6 Quia enim rectum motum non habet, patet, quoniam relinqueret medium, quod impossibile ostensum est. Si autem motum circularem haberet, super alium axem, quam mundi axem, variaretur altitudo poli. Si super axe mundi, quae sunt in aere relinqueretur versus occidentem, et aedificia corrueret.
7 Motus coelestes in duplici differentia reperiri. Nam motus primi mobilis, per quem Sol et astris omnia oriuntur et occidunt, et revolutionem in spacio diei naturalis perficiunt, omnibus cognitus est, quippe qui fit ab ortu in occasum super axe, polisque mundi. 8 Motus autem huic contrarius ab occasu ad ortum Solis, Lunae ac planetarum super axe zodiaci, patet ex quotidiana ipsorum observatione, et ortu atque occasu in diversis horizontis locis. Sequitur scientia chordarum.
Si aequilaterae figurae circulo inscribantur, hexagoni latus erit aequale semidiametro circuli. 9 Si autem huius lateris dimidium auferatur a linea potente latus ax dimidium ipsius, relinquetur latus decagoni. Cuius quadratum cum quadrato lateris hexagoni iunctam conficit quadratum lateris pentagoni. Porro quadratum lateris tetragoni duplum est, lateris vero trianguli triplum est ad quadratum lateris hexagoni. 10 Quadrata duarum chordarum (quarum arcus semicirculum2 integrat) similiter conflant quadratum diametri, quae est chorda semicirculi. Haec ex Euclide.[A:27r] Cum quadrilaterum circulo inscribitur, quod sub eius diametris continetur, aequale est aggregato eorum, quae sub oppositis lateribus.
11 Ex premissis, propositorum arcuum in semicirculo differentiae, dimidii et aggregati chorda notescet. Atque hinc multiplicatorum arcuum chordae, donec nota fiat chorda trium graduum, chorda graduum 11/2, et chorda 3/4 unius gradus, unde chorda unius gradus coniicietur. 12 Cum maior arcus ad minorem maiorem habeat rationem, quam chorda illius ad chordam huius. Hinc tabula chordarum per singula dimidia graduum, et per singulas graduum minutias. Et tabula sinus recti similiter exarabitur, ubi quo plures particulas habebit diameter, eo subtilior sequetur calculus in partibus graduum.
13 His autem praelibatis, Ptolemaeus exponit doctrinam sphaeralium triangulorum, ex Menelao geometra sumpta. Tebitius autem huiusmodi rudimenta multo facilius exposuit, Ptolemaeum carpens, sicut nos in traditione sphaericorum satis iam demonstravimus. Omissis ergo superfluis, summa sequar fastigia rerum.
14 Distantia duorum tropicorum est differentia duarum altitudinum solstitialium solis meridianarum per quadrantem observata. Cuius quidem dimidium est maxima Solis sive zodiaci ab aequatore declinato. Quae a Ptolemaeo inventa est graduum 23.51.20. Ab Albategnio graduum 23.35. Ab Alcmaeone graduum 23.331/2. 15 A Ioanne Regiomontio graduum 23.28.
In triangulo sphaerali orthogonio, sicut est sinus totus ad sinum anguli acuti, sic est sinus lateris rectum angulum subtendentis ad [A:27v] sinum lateris dictum angulum acutum respicientis. Quod facile ostenditur ex similitudine triangulorum sicut Tebitius fecit. 16 Ex quo theoremate, per tabulam sinuum, notescet declinatio et ascensio recta Solis per singula puncta zodiaci. Item in dicto triangulo sphaerali orthogonio habente duos angulos acutos, sinus aggregati laterum utrumlibet acutum continentium ad sinum differentiae eorumdem est sicut quadratum3 sinus complementi dimidii4 dicti acuti ad quadratum5 sinus, ipsius dimidii. 17 Unde quando aggregatum dictorum laterum est quadrans, tunc ipsorum differentia est maxima. Et sicut6 aggregatum ex sinu toto, sinuque secundo anguli acuti ad differentiam eorumdem. Et hinc sinus complementi reliqui lateris est medius proportionalis inter sinum totum et sinum complementi dicti acuti. 18 Quae consyderatio quamvis a Ptolemaeo praetermissa, in Sphaericis nostris plene discutitur et a Gebro acutissimo animadversa, et a Ioanne Regimontio in Tertio libro apposita. Hinc sequitur calculus omnis triangulorum sphaeralium.
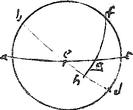
abcd meridianus, f polus, aec horizon, fc altitudo poli, bed aequator, g stella, ab vel cd altitudo aequatoris, gh declinatio, eg latitudo ortus, eh differentia ascensionalis