|
Propositio 51a
190
Omnis cubus aequalis est pyramidi hexagonae aequiangulae collaterali.
Exempli gratia, cubus quintus scilicet 125 qui et idem numerus est pyramis hexagona aequiangula quinta. Quod sic ostendam. Cubus quintus, per quadragesimam secundam, aequalis est aggregato columnarum triangularum quintae et quartae, necnon et trianguli quarti.
191
At per quadragesimam primam pyramis hexagona aequiangula quinta aequalis est aggregato pyramidis pentagonae quintae, pyramidis quadratae quartae, et pyramidis triangulae quartae. Demonstrandum est igitur nobis, quod haec duo praedicta aggregata sunt inter se aequalia; sic enim per173 communem animi conceptum sequetur174 ut cubus et pyramis hexagona aequiangula quinti loci sint invicem aequales.
192
Auferatur ab illo quidem aggregato columna triangula quinta; ab hoc vero aggregato pyramis pentagona quinta iampridem per ante praemissam aequales. Et demonstrandum erit quod duo residua inde, scilicet aggregatum columnae triangulae quartae et trianguli quarti; [S:22] hinc autem aggregatum pyramidis quadratae quartae et pyramidis triangulae quartae, sunt invicem aequalia; quod sic patet .
193
Per antepraemissam rursus, columna triangula quarta, aequalis est pyramidi pentagonae quartae; pyramis autem pentagona quarta, per trigesimam sextam, aequalis est pyramidi quadratae quartae et pyramidi triangulae [C:30v] tertiae.
194
Quamobrem, columna triangula quarta, una cum triangulo quarto, aequalis erit cumulo trium, scilicet pyramidis quadratae quartae, pyramidis triangulae tertiae et trianguli quarti. Ostendendum est igitur quod dictus cumulus aequalis est aggregato pyramidis quadratae quartae et pyramidis triangulae quartae.
195
Auferatur utrinque, scilicet tam ab illo cumulo, quam ab hoc aggregato, pyramis quadrata quarta, et demonstrandum supererit quod pyramis triangula tertia una cum triangulo quarto aequalis est pyramidi triangulae quartae; quod tandem constat per diffinitionem ipsius pyramidis triangulae; quippe quae assumpto semper sequenti triangulo procreat sequentem pyramidem. Qua argumentatione, sicut in quinto, ita175 in quolibet alio praecedenti vel sequenti loco, semper constabit propositum. Corollarium176
196
Quoniam igitur singuli cubi ab unitate ordinati sunt singulis pyramidibus hexagonis aequilateris ab unitate dispositis collateralibus aequales; propterea manifestum est quod cuborum differentiae sunt pyramidum praedictarum differentiis singulae singulis aequales, hoc est, ipsis hexagonis aequiangulis.
197
Ac, sicut ex talium hexagonorum ad unitatem successiva coacervatione pyramides praedictae per ordinem construuntur, ita et177 cubi procreantur. Suntque ipsi hexagoni cuborum gnomones ab unitate continuati.
|
|
|
cubus 5us 125 |
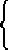 |
col. triangula. 5a 75 |
|
col. triangula 4a 40 |
|
triangulus 4us 10 |
|
|
|
|
|
pyr. hexag. aequiangula 5. 125 |
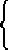 |
pyr.  na 5a 75 na 5a 75 |
pyr.  ta 4a 30 ta 4a 30 |
pyr.  la 4a 20 la 4a 20 |
|
|
|
|
col. triang. quarta 40  pyr. pyr.  na 4a 40 na 4a 40 |
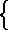 |
pyr.  ta 4a 30 ta 4a 30 |
pyr.  la 3a 10 la 3a 10 |
|
|
 lus 4us 10 lus 4us 10   lus 4us 10 pyr. lus 4us 10 pyr.  ta 4a 30 ta 4a 30  pyr. pyr.  ta 4a 30 ta 4a 30 |
|
pyr.  la 3a 10 la 3a 10 |
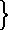 |
pyr.  la 4a 20 la 4a 20 |
 lus 4us 10 lus 4us 10 |
|
|
|