F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de lineis spiralibus liber 3
<- App. -> <- = ->

PROPOSITIO III

22 A centro circuli ad lineam rectam, quae circulum tangit, duci potest recta, ita ut ductae pars inter tangentem et peripheriam, ad semidiametrum circuli minorem habeat rationem, quam peripheriae pars inter contactum et ductam intercepta ad quamcumque peripheriae partem.

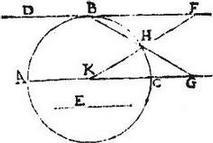
figura 3

23 Esto circulus ABC, centrum K, tangens DF, punctum contactus B, detur quaecumque pars peripheriae, qua potest sumi recta linea maior quae sit E; et recta AKG aequidistet tangenti et HG ponatur ipsi E aequalis, et tendens ad punctum B, secans peripheriam in H, et per K et H ducta KHF, occurrat ipsi DF ad punctum F. Itaque, propter similitudinem triangulorum, sicut FH ad HK, sic BH ad HG. 24 Igitur minor est ratio FH ad HK, [S:198] quam BH peripheriae ad HG, et a fortiori minor est ratio FH ad HK, quam BH peripheriae ad datam peripheriam; quandoquidem HG, hoc est ipsa E, maior fuit quam data peripheria.

Inizio della pagina
 ->