PROPOSITIO IV

25 A centro circuli, secans collocatam in circulo, recta linea potest duci ad peripheriam, ita ut pars ductae inter peripheriam et collocatam, ad lineam connectentem terminos illarum in peripheria, rationem habeat datam. 26 Oportebit autem rationem datam minorem existere ratione quam habet dimidium collocatae ad perpendicularem a centro ad collocatam.

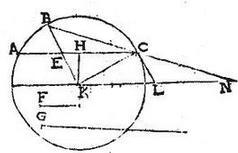
27 Esto circulus ABC, centrum K, collocata AC, per medium secta apud H, et habeat F ad G minorem rationem quam CH ad HK; sit KN aequidistans ipsi AC, angulus KCL rectus. Quare propter similitudinem triangulorum sicut est CH ad HK, sic KC ad CL, igitur KC ad CL maiorem rationem habet, quam F ad G. 28 Itaque sicut F ad G, sic sit KC ad BN, quae utique maior erit, quam CL. Et ideo, BN ducta per punctum C, ita locari poterit, ut ipsi KN occurrens apud N rursum peripheriae incidat apud punctum B, et ducatur KB secans ipsam AC apud E. 29 Et quoniam fuit sicut F ad G, sic KC, hoc est BK, ad BN, erit propter similitudinem triangulorum, et EB ad BC, sicut F ad G. Quod possibile factu fore diximus.