PROPOSITIO XII

92 Si recta secet per aequalia trianguli rectilinei angulum, latera, quae angulum illud continet, sunt plusquam duplum lineae secantis.

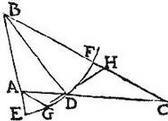
93 In triangulo rectilineo ABC, recta BD secet angulum ABC per medium. Aio quod latera AB, BC simul sumpta sunt plusquam duplum lineae BD. Nam si linearum AB, BC utraque sit maior quam BD, vel una aequalis, et altera maior, constat propositum (ambae enim minores nequeunt esse). 94 Si autem linearum AB, BC altera minor, altera maior sit quam BD, tunc sit minor AB et maior BC, et super centrum B, spatiumque BD circuli peripheria describatur EDF, secans quidem ipsam BC apud F, ipsique BA productae occurrent apud E, et aequidistans ipsi BC ducatur AG, et ducatur GDH. 95 Eruntque triangula ADG, CDH similia: cumque DH sit longior quam chorda DF, et perinde longior quam chorda DG, erunt et caetera latera trianguli CDH caeteris lateribus trianguli ADG singula singulis maiora: et ideo CH longior quam AG, et a fortiori longior quam AE, et eo magis CF longior quam AE. 96 Maior igitur excessus lineae BC super lineam BD, quam excessus ipsius BD super lineam BA. Quare AB, BC, simul sumptae lineae conficiunt plusquam duplum lineae BD. Quod fuit demonstrandum.