PROPOSITIO VII.
Coni-coluri curva superficies aequalis est ei, quod fit ex latere ipsius coni in dimidias basium peripherias.
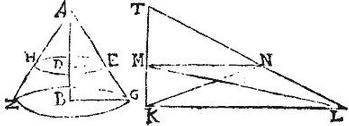
Sit trigonum ABG rectum, qui apud B angulum habens, et DE ipsi BG parallelus; et circumducto triangulo ABG semel circum axem AB, sit a trigono ABG descriptus conus AGZ basim habens, circulum GZ, qui vero a trigono ADE conus describitur, sit AHE basim habens circulum HE, horum autem conorum differentia quae scilicet describitur a trapezio DBGE, vocatur colurus-conus; habetque duas bases inaequales circulos scilicet GZ, EH. Aio itaque quod curva superficies coni-coluri, quae scilicet describitur a linea EG, aequalis est ei, quod fit ex ipsa linea EG in dimidias peripherias circulorum GZ, EH. Exponatur enim trigonum TKL rectum, qui apud K angulum habens, cuius latus TK sit ipsi AG hypothemisae, latus vero KL ipsi GZ peripheriae aequale, eritque per 2. huius, coni AGZ curva superficies aequalis trigono TKL, ponatur ipsi GE aequalis KM, et ducatur ipsi KL parallelus MN, eritque, propter triangulorum similitudinem, sicut TK ad TM, et ideo sicut GA ad AE, et ideo sicut semidiameter BG ad semidiametrum DE, sic KL ad MN: sed per praemissam, sicut BG semidiameter ad DE semidiametrum, sic GZ peripheria ad EH peripheriam. Igitur sicut GZ peripheria ad EH peripheriam, sic KL ad MN; et permutatim sicut peripheria GZ ad KL sic peripheria EH ad MN; aequalis autem est peripheria GZ lineae KL: ergo et peripheria HE aequalis lineae MN. Et quoniam TM aequalis ipsi AE, ideo per 2. huius, superficies coni AHE aequalis est trigono TMN; fuit autem curva superficies coni AZG aequalis trigono TKL: ergo curva superficies coni-coluri EZ aequalis erit trapezio KMNL.
Connectantur itaque KN, ML, eruntque per 7.1. triangula KML, KNL aequalia invicem: sed quod fit ex KM in KL est duplum trianguli KML: ergo, et duplum trianguli KNL; quod autem fit ex KM in MN duplum est trianguli KMN: igitur quod fit ex KM in ipsas KL, MN duplum est totius trapezii KMNL: itaque quod fit ex KM in dimidium ipsarum KL, MN, aequum est trapezio KMNL: verum KM fuit aequalis ipsi EG, ipsa autem KL aequalis peripheriae ZG, ipsa vero MN aequalis peripheriae EH: ergo quod fit ex EG in dimidias peripherias circulorum GZ, EH aequum est trapezio KMNL: et ideo curvae superficiei coni-coluri EZ, cui fuit trapezium aequale: et hoc erat demonstrandum.
COROLLARIA.
Itaque quod fit ex aggregato semidiametrorum basium coni-coluri in peripheriam cuius diameter est latus conicum aequale est superficiei conicae, quod sequitur ex 2. et 3. corollario secundae. [S:49]
Adhuc et circulus, cuius semidiameter est media proportionalis inter latus coni-coluri, et aggregatum ex semidiametris basium, aequalis est conicae superficiei; quod sequitur ex postremo corollario primae.