PROPOSITIO IV.

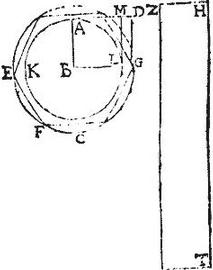
Cylindri curva superficies aequalis est rectangulo sub lateribus contento, quorum unum axi cylindrico, reliquum vero peripheriae basis est aequale.

Sit parallelogrammum rectangulum ABGD quo semel revoluto circa latus AB fixum, describatur cylindrus axem habens AB, basim vero circulum GE: sitque rectangulum ZHT, cuius latus quidem ZH axi AB, latus vero HT peripheriae circuli EG sit aequale. Aio quod cylindrica superficies, quam describit latus GD aequalis est rectangulo ZT. Nam si rectangulum ZHT non sit aequum cylindricae superficiei, quam describit linea DG, erit aequum cylindricae superficiei alicuius cylindri ha[S:44]bentis basim maiorem, minoremve circulo EG circa eundem axem AB: sit ergo primum rectangulum ZHT aequum curvae superficiei cylindri, cuius basis sit circulus KL minor circulo EG, et axis idem AB, qui scilicet cylindrus a rectangulo ABLM circa axem AB circumducto describitur, et cuius curva superficies describitur a linea LM: et per 13.12. inscribitur circulo EG polygonium EG laterum aequalium minime contingentium circulum KL, super quod polygonium erigatur prisma eandem cum cylindro habens celsitudinem, ductis lateribus cylindri super angulos polygonii perpendicularibus, eruntque parallelogrammata prismatis, quorum bases sunt latera polygonii simul aequalia per 36.1. vel per 1.6. rectangulo quod fit ex axe AB in perimetrum polygonii EG: sed hoc rectangulum minus est rectangulo ZT, quod fit ex axe AB in peripheriam circuli EG, quae maior est perimetro polygonii: rectangulum autem ZT aequum fuit superficiei cylindricae, quam describit linea LM: igitur parallelogrammum prismatis, cuius basis polygonium EG minus est quam superficies cylindrica, quam describit linea LM; superficies inquam claudens minor est inclusa, quod est impossibile.

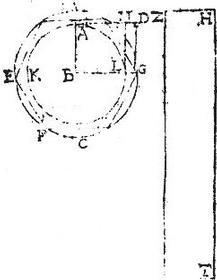
Vel sic quoniam rectangulum ZT maius est rectangulis prismatis praedictis, rectangula vero prismatis maiora, quam superficies cylindrica, quam describit linea LM, quandoquidem includens inclusa maior; ideo rectangulum ZT maius superficie cylindrica, quam describit linea LM: quare non ei aequale sicut proponebatur. Esto nunc rectangulum ZHT aequum, si possibile est, cylindricae superficiei cylindri habentis basim maiorem circulo EG, et axem AB. Sitque brevitatis causa, cylindrus suppositus, cuius axis AB, et basis circulus KL, qui scilicet describitur a rectangulo ABLM circumducto semel circa axem AB, et rectanguli ZT latus ZH aequum axi AB, et latus HT aequum peripheriae circuli KL. Aio iam quod non est possibile rectangulum ZT esse aequum superficiei curvae alicuius cylindri circum axem AB descripti, et habentis basim maiorem circulo KL. Nam si possibile est, sit rectangulum ZT aequum superficiei curvae cylindri, cuius basis circulus EG maior circulo KL, qui scilicet a rectangulo ABGD circum axem AB revoluto, et cuius superficies curva a linea GD describitur: et inscribatur ut prius circulo EG polygonium aequalium laterum non tangentium circulum KL, et super polygonium prisma inclusum cylindricae superficiei, quam describit linea GD: eruntque prismatis rectangula, quorum bases sunt latera polygonii simul aequalia per 36.1. vel 1.6. rectangulo, quod fit ex axe AB in perimetrum polygonii EG: hoc itaque rectangulum maius est rectangulo ZT, quoniam illius unum latus aequale uni lateri huius, et reliquum reliquo maius (maius enim perimeter polygonii EG, quam peripheria KL) sed rectangulum ZT aequum fuit superficiei cylindricae, quam describit linea GD. Ergo dicta prismatis rectangula simul maiora sunt superficie cylindrica, quam describit linea GD: superficies itaque inclusa prismatis maior superficie cylindrica claudente, quod est impossibile: non est igitur rectangulum ZT aequum alicui curvae superficiei cylindri circum axem AB, cuius basis sit maior circulo KL. [S:45]

Similiter ergo si rectanguli ZT latus ZH axi AB, et latus HT peripheriae circuli EG sit aequale: non erit rectangulum ZT aequum superficiei curvae cylindri cuiuspiam circum axem AB, cuius basis sit maior circulo EG: fuitque ostensum quod, nec idem rectangulum aequum est superficiei curvae cylindri cuiuspiam circum axem AB, cuius basis sit minor circulo EG: superest ergo ut idem rectangulum ZT aequale sit superficiei curvae cylindri, cuius axis AB, basisque circulus EG, quam scilicet superficiem describit linea GD, quod est propositum.

COROLLARIUM I.

Manifestum est ergo quod cylindrica superficies producitur ex axe cylindrico in peripheriam basis.

COROLLARIUM II.

Rursum ex ductu diametri cylindricae basis in peripheriam circuli, cuius diameter est cylindricus axis, producitur cylindrica superficies, quod sequitur ex tertio corollario primae.

Demum circulus, cuius semidiameter est media proportionalis inter latus seu axem cylindricum, ac diametrum cylindricae basis, superficiei cylindricae aequalis est; quod sequitur ex postremo corollario primae.