PROPOSITIO XXXVIII.

Sphaera ad cubum suae diametri rationem habet, quam undecim ad unum, et viginti fere.

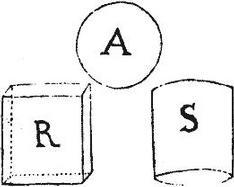
Sit sphaera A, cubus R, cuius latus aequum sit diametro sphaerae A. Aio quod sphaera A ad cubum R est fere sicut 11. ad 21. quod sic concludam. Sit cylindrus S, cuius basis diameter diametro sphaerae A, et celsitudo eidem diametro sit aequalis. Itaque prismatis R, et cylindri S celsitudo est una. Quare per corollarium 33. huius erit sicut basis prismatis R ad basim cylindri S, sic prisma R ad cylindrum S: sed basis prismatis R est quadratum, quod ex diametro basis cylindri S; estque per 8. de dimensione circuli. quadratum, quod ex diametro circuli ad circulum sicut 14. ad 11. fere. Igitur prisma R ad cylindrum S est fere sicut 14. ad 11. per corollarium autem 26. huius, vel per 28. cylindrus S sesquialter est ad sphaeram A: et ideo sicut 21. ad 14. Ergo per 23.5. ex aequa proportione erit sicut 21. ad 11. Sic cubus R ad sphaeram A: quod est propositum. [S:85]

COROLLARIUM I.

Manifestum est ergo quod 21. sphaerae sunt aequales 11. cubis, qui fiunt ex diametro sphaerae: patet nam per praemissam; sphaera ad cubum suae diametri est sicut 11. ad 21. Ergo per 13. quinti 11. sphaerae ad 11. cubos sunt sicut 11. ad 21. Ergo conversim 11. cubi ad 11. sphaeras sunt sicut 21. ad 11. sed 21. sphaerae ad 11. sphaeras sunt sicut 21. ad 11. Igitur 21. sphaerae eam habent rationem ad 11. sphaeras, quam 11. cubi ad easdem 11. sphaeras: quare per 9. quinti 21. sphaerae aequales sunt 11. cubis, qui ex diametro sphaerae.

COROLLARIUM II.

Unde manifestum est si cubus, qui ex diametro cuiuspiam sphaerae multiplicetur undecies, producti pars 21. erit solidum sphaerae: contra si sphaera vicies semel multiplicetur producti pars 11. erit cubus, qui ex diametro sphaerae. Sed haec supponunt rationem peripheriae ad diametrum triplam sesquiseptimam: quod si peripheriae ad diametrum ratio supponatur tripla superpartiens 10/71 quoniam tunc per 8. de dimensione circuli, quadratum, quod ex diametro circuli ad ipsum circulum est sicut 284. ad 223. et per 28. huius, sphaera ad cylindrum est sicut 426. ad 284. scilicet sesquialtera. Ideo ex 23.5. ex aequa perversim proportione, erit sicut 426. ad 223. Sic cubus R ad sphaeram A. Quamobrem tunc 426. sphaerae erunt aequales cubis 223. qui fiunt ex diametro sphaerae, quod sequitur ex dicta argumentatione: unde si cubus, qui ex diametro sphaerae multiplicetur 223. producti pars 426. erit solidum sphaerae. Contra si sphaera 426. multiplicetur, producti pars 223. erit cubus, qui ex diametro sphaerae. Verum prima suppositio, quae facit peripheria ad diametrum esse triplam sesquiseptimam, facit et sphaeram aliquanto maiorem vero; altera autem, quae peripheriam ad diametrum profert triplam super partientem 10/71 facit sphaeram aliquanto minorem veritate. Non enim licuit in hoc punctum geometricum attingere, non ipsi quidem Archimedi, quamvis geometrarum omnium acutissimo.