PROPOSITIO XXV.
Sphaera aequalis est cono, cuius basis sphaericae superficiei, celsitudo vero sphaerae semidiametro aequalis est.
Sit circulus ABGD, cuius centrum E, diameter AG, et circumacto semel semicirculo ABG super immotam diametron AG describatur sphaera ABG, sitque conus M, cuius basis sphaerae ABG superficiei, celsitudo autem semidiametro AE sit aequalis. Aio quod aequalis est conus M sphaerae ABG: nam si conus M non sit aequalis sphaerae ABG erit aequalis sphaerae alteri alicui maiori, vel minori, quam est ipsa sphaera ABG. Sit ergo primum, si possibile est, conus M aequalis sphaerae ZHT minori quam est sphaera ABG, et cum ea concentricae, cuius diameter ZT, et quam circa diametrum ZT revolutus describit semicirculus ZHT, et per 13.12. inscribatur circulo ABG polygonium aequalium laterum minime tangentium circulum ZT, quod sit ABGD, cuius laterum unum sit AK ad quod a centro perpendicularis exeat EL, et polygonii dimidio semel circa diametrum AG circumacto describatur solidum co[S:71]nicarum superficierum minime iam tangentium sphaeram ZHT, eritque per praecedentem, solidum ABG aequum cono, cuius basis aequalis est superficiei solidi ABG, celsitudo vero perpendiculari EL, huiusmodi itaque cono maior est conus M, quandoquidem, et basi, et celsitudine superior est, quoniam scilicet sphaerae ABG superficies maior est solidi ABG inclusi superficie, et linea AE maior, quam perpendicularis EL: et ideo sphaera ZHT ipsi cono M aequalis maior erit solido ABG: pars toto, quod est impossibile. Vel sic, quoniam conus M maior fuit cono dicto aequali ipsi solido ABG, et ideo maior ipso solido ABG; et solidum ABG maius sphaera ZHT: propterea conus M maior erit sphaera ZHT, non est ergo ei aequalis sicut supponebatur.
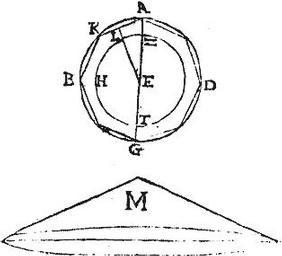
Sit deinde, si possibile est, conus M aequalis sphaerae maiori, quam est sphaera ABG: sed brevitatis causa, sit supposita ipsa ZHT, et conus M basim habeat aequalem superficiei sphaerae ZHT, celsitudinem vero aequalem semidiametro EZ. Aio quod conus M non erit aequalis sphaerae alicui maiori, quam est sphaera ZHT. Nam si possibile est, sit aequalis sphaerae ABG maiori. quam est sphaera ZHT, et cum ea concentricae; describatur intra sphaeram ABG solidum ABG ut prius, cuius superficies non tangat sphaeram ZHT etc. Eritque per praecedentem solidum ABG aequum cono, cuius basis aequalis est superficiei solidi ABG, et celsitudo perpendiculari EL: talis ergo conus maior cono M, quem et basi, et celsitudine superat: quare solidum ABG maius cono M. Sed conus M, per hypothesim, aequalis fuit sphaerae ABG: ergo solidum ABG maius quam sphaera ABG: pars toto, quod est impossibile: non est ergo conus M aequalis alicui sphaerae maiori quam est sphaera ZHT. Similiter si conus M basim superficiei sphaerae ABG, et celsitudinem aequam semidiametro EA non erit aequalis sphaerae cuiquam maiori, quam est sphaera ABG; fuitque ostensum, quod nec minori: superest ergo ut aequalis omnino sit conus M sphaerae ABG: quod erat demonstrandum.
Manifestum est ergo, quod sphaera aequalis est cono, cuius basis semidiameter aequalis est diametro sphaerae, axis vero semidiametro sphaerae. Patet: nam per corollarium 10. circulus, cuius semidiameter aequalis diametro sphaerae, est aequalis superficiei sphaerae.