PROPOSITIO II.

Coni curva superficies aequalis est trigono rectangulo, cuius unum laterum rectum angulum continentium aequale est conico lateri, reliquum vero peripheriae basis.

Sit trigonum rectangulum ABG rectum, qui ad B angulum habens, quo super axem AB revoluto donec redeat ad locum suum, describatur conus verticem habens A, basim vero circulum GDE, sitque trigonum ZHT rectum apud H angulum habens, cuius latus ZH ipsi hypothemisae AG sit aequale; latus autem HT peripheriae circulari GDE aequalis.

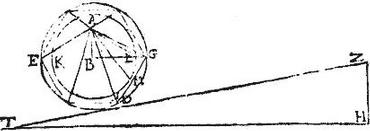
Dico, quod conica superficies coni AGDE, quam describit linea AG aequalis est trigono ZHT. Nam si trigonum ZHT non sit aequum conicae superficiei AGDE, erit omnino aequum conicae superficiei coni habentis basim minorem, maioremve circulo GD, et altitudinem eandem cum cono AGD. Sit ergo primum trigonum ZHT aequum conicae superficiei coni, cuius vertex A basisque circulus KL minor ipso circulo EG, et latus AL, qui videlicet conus ab ipso trigono ALB describitur, et per 13.12. intra circulum EG describatur polygonium rectilineum aequilaterum, et aequiangulum, cuius latera minime contingant circulum KL, et a vertice A descendant hypothemisae ad angulos polygonii, quae cum lateribus polygonii continebunt pyramidem habentem cum cono AGD verticem eundem, et inclusam eidem cono: itaque ducatur a vertice A perpendicularis ad unum laterum polygonii EG ut pote ad latus GD, quae perpendicularis sit AM, eritque per praecedentem superficies pyramidis AGD, quae congeries est trigonorum ad verticem A coeuntium, aequalis trigono rectangulo, cuius unum latus eorum, quae circa rectum, aequale est perpendiculari AM, reliquum perimetro polygonii GDE: huiusmodi ergo trigonum minus est trigono ZHT, cuius latera ZH, HT, quae circa rectum maiora sunt, quippe quae aequalia sunt lateri AG, et peripheriae circuli GDE, quae maiora sunt perpendiculari AM, et perimetro polygonii GDE, sed trigonum ZHT aequum fuit superficiei coni ALK: igitur superficies dicta pyramidis AGD minor est superficie coni ALK: quod est impossibile; cum superficies pyramidis maior sit superficiei coni ALK inclusa. Vel sic quoniam trigonum ZHT maius est trigono, cui aequalis est superficies pyramidis; superficies autem pyramidis maior est superficie coni ALK inclusa: ergo trigonum ZHT maius est superficie coni ALK; itaque non est ei aequale, sicut supponebatur. Esto nunc trigonum ZHT aequum, si possibile est, conicae superficiei coni habentis basim maio[S:42]rem circulo GD, et eandem altitudinem cum cono AGD: sitque, brevitatis causa, conus suppositus ALK, et trigoni ZHT latus ZH aequum hypothemisae AL, at latus HT aequum peripheriae circuli KL. Aio iam, quod non est possibile trigonum ZHT esse aequum superficiei curvae alicuius coni habentis basim maiorem circulo KL, et verticem A.

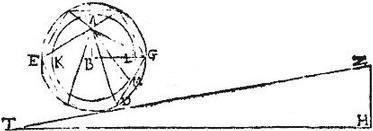
Nam si possibile est, sit trigonum ZHT aequum superficiei coni, cuius basis circulus EG maior circulo KL, et describatur ut prius intra circulum EG polygonium aequalium laterum non tangentium circulum KL, et super polygonium pyramis GD vertice A, a quo ad unum laterum polygonii DG cadat perpendicularis AM, eritque per praecedentem superficies pyramidis AGD, quae congeries est trigonorum ad verticem, aequalis trigono rectangulo, cuius laterum, quae circa rectum unum aequale est perpendiculari AM, reliquum perimetro polygonii GDE; hoc itaque trigonum maius est trigono ZHT cum habeat latera, quae circa rectum maiora; sed trigonum ZHT aequum fuit superficiei coni AGDE: ergo dicta pyramidis superficies maior est superficie coni AGDE inclusa claudente, quod est impossibile. Similiter ergo si trigoni ZHT latus ZH hypothemisae AG, et latus HT peripheriae circuli EG sit aequale, non esset trigonum ZHT aequale superficie coni cuiuspiam, cuius basis sit maior circulo EG, et vertex A, fuitque ostensum, quod nec idem trigonum aequum est superficiei coni cuiuslibet, cuius basis sit minor circulo EG, et vertice A, superest ergo ut idem trigonum ZHT aequum sit conicae superficiei coni AGDE, quod erat demonstrandum.

COROLLARIUM I.

Manifestum est ergo quod ex ductu conici lateris in dimidium periphaeriae basis producitur conica superficies; quemadmodum ex ductu unius laterum, quae circa rectum, in trigono rectangulo, in reliqui dimidium per 41.1. consurgit area trigoni.

COROLLARIUM II.

Rursum ex ductu semidiametri conicae basis in semiperipheriam circuli, cuius semidiameter est latus conicum producitur conica superficies, quod sequitur ex tertio corollario primae.

COROLLARIUM III.

Demum circulus, cuius semidiameter est media proportionalis inter latus conicum, ac semidiametrum conicae basis aequalis est conicae superficiei; quod sequitur ex postremo corollario primae.