PROPOSITIO XIX.

Si sphaera duobus parallelis planis secetur intercepti segmenti sphaerica superficies, zona scilicet sphaerica, aequalis est ei, quod fit ex diametro sphaerae in peripheriam circuli, cuius diameter est axis segmenti.

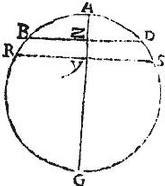
Praeteritae descriptioni addo rectam RS ad rectos angulos secantem diametrum AG in puncto Y: itaque RY in circumductione semicirculi describet circulum parallelum circulo, cuius diameter BD. Aio itaque quod segmenti sphaerici BS, quod inter duos circulos parallelos, quorum diametri BD, RS intercipitur, sphaerica superficies, quae quasi zona est ab arcu BR descripta; aequalis est ei, quod fit ex diametro AG in peripheriam circuli, cuius diameter est axis ZY: nam per 15. praemissam, quod fit ex AG in peripheriam circuli, cuius diameter AY aequum est sphaericae superficiei segmenti RAS: peripheria autem cir[S:63]culi, cuius diameter AY aequalis est per primum corollarium sextae. peripheriis circulorum, quorum diametri AZ, ZY: ergo quod fit ex AG in peripherias circulorum, quorum diametri AZ, ZY aequum est sphaericae superficiei segmenti RAS: verum per 15. quod fit ex AG in peripheriam circuli, cuius diameter AZ aequum est sphaericae superficiei segmenti BAD: itaque de eo, quod ex AG in peripherias circulorum, quorum diametri AZ, ZY dematur id, quod ex AG in peripheriam circuli, cuius diameter AZ; item de superficie sphaerica segmenti RAS dematur superficies sphaerica segmenti BAD (duo scilicet aequalia de duobus aequalibus) et supererit, inde, id, quod ex AG in peripheriam circuli, cuius diameter ZY; hinc autem id, quod superficies sphaerica segmenti intercepti BS. et per consequentiam aequalia: quod est propositum. Idem ostendes per corollarium 15. Nam per illud ex linea AY in peripheriam circuli ABG, fit superficies sphaerica segmenti RAS: ex linea autem AZ in peripheriam eandem fit superficies sphaerica segmenti BAD: unde sequitur ex prima 2. elementorum, ut ex ZY in dictam peripheriam fiat superficies sphaerica segmenti BS intercepti. Quod est propositum.

COROLLARIUM I.

Manifestum est ergo quod sphaerici segmenti parallelis circulis interclusi sphaerica zona aequalis est ei, quod fit ex axe segmenti in peripheriam circuli maximi in sphaera; et ideo curvae superficiei cylindri, cuius basis est circulus maximus sphaerae, celsitudo autem axis segmenti.

COROLLARIUM II.

Item manifestum est, quod parallelis planis quotcumque sphaeram secantibus, sphaericae superficies planis interceptae sunt ad invicem sicut ipsorum sphaeralium segmentorum axes: patet hoc ex corollario praecedentis, et prima sexti Elementorum. Poterat et hoc corollarium demonstrari per corollarium 17. praeteritae. ex aequa, et disiuncta proportione facillime.