PROPOSITIO XVIII.
Si sphaera plano secetur, utriuslibet segmenti sphaerica superficies ad circulum secantem, est sicut diameter sphaerae ad axem reliqui segmenti.
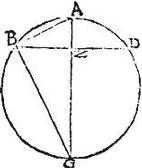
Adhuc manebo in eadem descriptione dicens, quod sphaerica superficies segmenti BAD ad circulum, cuius diameter BD secantem, est sicut diameter AG ad axem GZ. Item quod sphaerica superficies segmenti BGD ad circulum, cuius diameter BD est sicut diameter AG ad axem AZ: nam per 8. sexti ratio AG ad GZ est dupla eius, quae AG ad GB; sed AG ad GB, sicut AB ad BZ, propter similitudinem triangulorum AGB, ABZ: ergo ratio AG ad GZ dupla est eius, quae AB ad BZ: sed et eius, quae AB ad BZ dupla est per 2.12. quae circuli, cuius semidiameter AB ad circulum, cuius semidiameter BZ: igitur circulus, cuius semidiameter AB ad circulum, cuius semidiameter BZ est sicut AG ad ZG; fuit autem per 16. circulus, cuius semidiameter AB aequalis superficiei sphaericae segmenti BAD, circulus vero, cuius semidiameter BZ aequalis est circulo BD sphaeram secante: ergo sphaerica superficies segmenti BAD ad circulum, cuius semidiameter BZ, (qui segmenta disterminat,) est sicut AG diameter ad axem GZ reliqui segmenti. Non aliter ostendam quod sphaerica superficies segmenti BGD ad circulum, cuius semidiameter BZ est sicut diameter AG ad axem reliqui segmenti AZ: quod est propositum.