F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Praeparatio ad Archimedis opera 27
<- App. -> <- = ->

PROPOSITIO XXVII.

Idem aliter demonstrare.

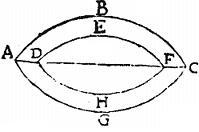
figura 17

Sunto datae lineae AB, BC, et compleatur rectangulum ABCD, cui per nonam 4. Euclidis circulus circumscribatur: mox inter BA, BC, indefinitum productas deducatur recta FDHG, hac conditione, ut ipsae FD, HG sint inter se aequales; tunc enim CF, AG erunt inter ipsas AB, BC datas mediae proportionales. Nam per 35. tertii Euclidis, rectangulum AG, GB aequale est rectangulo HG, GD, et rectangulum CF, FB aequale est rectangulo DF, FH; sed rectangulum DF, FH aequale est rectangulo HG, GD; quandoquidem DF, GH lineae supponuntur aequales: igitur rectangulum CF, FB aequale est rectangulo AG, GB: quare per xv. sexti, non aliter quam in praecedenti, ex similitudine ipsa triangulorum demonstrabuntur AB, CF, GA, BC, continue proportionales. Et hic est modus Apollonii, et Philonis Byzantii, ut testatur Ioannes Philoponus Alexandrinus. Et est idem ferme cum modo Heronis: quamvis demonstrationes aliquantum differant.

Inizio della pagina
 ->