PROPOSITIO XXVI.

Quibuslibet duabus lineis duas medias esse proportionales.

Sint quaelibet datae lineae rectae AB, BC, compleatur rectangulum ABCD, et BC, BA producantur indefinitae, centrumque rectanguli sit E, in quo se vicissim secant diametri AC, BD: productis autem BA, BC applicetur per D ducta recta FDG, hac conditione, ut coniunctae EF, EG sint aequales: aio tunc, CF, AG medias proportionales interiacere ipsis AB, BC.

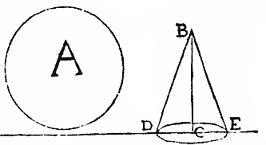
Ducantur enim EH, EK perpendiculares ad AB, BC; eritque per sextam secundi Euclidis rectangulum BF, FC cum quadrato KC sumptum aequale quadrato KF; commune ponatur quadratum EK. Eritque rectangulum BF, FC cum quadrato KC, et quadrato KE, hoc est cum quadrato EC sumptum aequale quadrato KF, cum quadrato EK, hoc est quadrato EF. Similiter omnino demonstrabimus, quod rectangulum BG, GA, cum quadrato EA sumptum, aequale est quadrato EG: aequalia vero sunt per hypotesim quadrata EF, EG: igitur rectangulum BFC cum quadrato EC aequal est rectangulo BGA cum quadrato EA. Item quadrata EC, et EA sunt aequalia quoniam dimidiis eiusdem AC lineae debentur; supe[S:15]rerunt ergo rectangulum BF, FC et rectangulum BG, GA inter se aequalia. Quare per 15. sexti Euclidis, sicut BG ad BF, sic FC ad GA. Et propter similitudinem, triangulorum GBF, DCF, sicut DC, hoc est, AB ad CF, sic FC, ad GA. Item propter similitudinem triangulorum GAD, DCF, sicut DC, ad CF, sic GA, ad AD, hoc est ad BC. Itaque quatuor lineae AB, CF, GA, BC sunt continuae proportionales. Et hoc proponebatur demonstrandum.

Et hic quidem est modus Heronis, qui Mechanica scripsit. Subiiciemus nunc aliorum philosophorum circa idem problema ex Eutocio sumptas traditiones.