PROPOSITIO XXVIII.

Aliter idipsum ostendere.

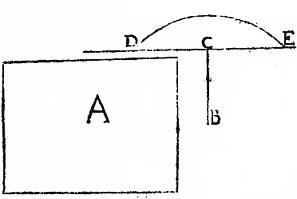
Sunto datae rectae AB, BG ad angulum rectum positae: quae producantur, sintque BE, BD singulae ipsi AB aequales, ad cuius spatium super centro B describatur semicirculus ADE, coniunctaque AG producatur ad peripheriam in punctum Z, et circa punctum E moveatur canon ET donec portio canonis TK inter peripheriam, et AZ per aequalia secetur ab ipsa BD in puncto L. [S:16] Et per punctum K ipsi BD parallelus agatur MN, sitque sicut MA ad AB, sic EM ad MX: itemque sic NM ad MO. Dico itaque quod BG, MX, MO, AB lineae sunt continuae proportionales. Agatur enim ipsi BD parallelus TP; eruntque BP, BM aequales, quandoquidem TL, LK iisdem parallelis interpositae fuerunt inter se aequales: quare KM ad ME, sicut TP ad PE; et ideo sicut NM ad MA; et ideo sicut ME ad MN: quandoquidem MN media proportionalis est inter ipsas AM, ME; igitur, et ME ipsis KM, MN media proportionalis est. Non dubium ergo, quin KM, ME, MN, MA sint in proportione continua; sed sicut BG ad KM, sic AB ad MA, propter similitudinem triangulorum: itemque per hypothesim, sicut MX ad ME, et sic MO ad MN. Ergo ex permutata proportione sequitur, ut ipsae quoque lineae BG, MX, MO, AB sint in eadem continua proportione. Quod erat demonstrandum. Est autem haec traditio Pappi in Mechanicis. Et hac eadem uti videntur Diocles, et Porus.