PROPOSITIO XVIII.

Sphaerarum superficies sunt quadratis diametrorum proportionales.

Sint duae sphaerae AIB, et CKD, quarum diametri AB, CD; sitque, per primam huius, sicut sphaerica superficies AIB ad sphaericam superficiem CKD. Sic qua[S:10]dratum AB ad quadratum EF. Et demonstrandum erit, quod linea EF aequalis est lineae CD.

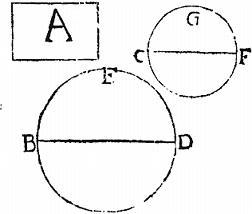
Nam si possibile est, sit maior linea EF, quam linea CD; et circa diametrum EF sphaera ELF intelligatur concentrica sphaerae CKD, et intra sphaeram ELF solidum ENF tornatile ex conicis superficiebus sphaeram CKD minime tangentibus: et huic simile solidum AMB intra sphaeram AIB; eritque per praecedentem, sicut quadratum AB, ad quadratum EF, sic superficies solidi AMB, ad superficiem solidi ENF; et ideo, sicut sphaerica superficies AIB, ad sphaericam superficiem CKD, et permutatim, sicut superficies solidi AMB, ad sphaericam superficiem AIB, sic superficies solidi ENF, ad superficiem sphaericam CKD; sed per quartum postulatum, maior est superficies sphaerica AIB, quam superficies solidi AMB: ergo, et superficies sphaerica CKD maior, quam superficies solidi ENF; quod est impossibile per dictum postulatum. Non est ergo maior linea EF, quam linea CD. Si autem sit minor, tunc conversim erit sicut sphaerica superficies CKD ad sphaericam superficiem AIB, sic quadratum EF ad quadratum AB; sit ergo per septimam huius, sicut quadratum EF ad quadratum AB, sic quadratum CD ad quadratum GH; eritque sicut quadratum CD ad quadratum GH, sic iam superficies sphaerica CKD, ad superficiem sphaericam AIB: et quoniam CD maior, quam EF, iam per decimam quartam quinti, erit, et GH maior, quam AB: unde sequitur idem impossibile, quod prius, ut scilicet sphaericae superficiei primae ad sphaericam superficiem secundam ratio sit, sicut quadratum primae diametri ad quadratum lineae maioris secunda diametro. Non est ergo minor linea EF, quam linea CD: sed nec maior fuit: aequalis ergo erit: quod fuit demonstrandum.