F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Praeparatio ad Archimedis opera 15
<- App. -> <- = ->

PROPOSITIO XV.

Cuivis datae lineae alicuius circuli peripheriam esse aequalem.

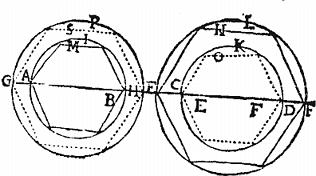
figura 9

Esto quaevis data linea A; describatur super quamvis lineam BD circulus BED, cuius peripheria si aequalis sit lineae A constat propositum. Sin vero, tunc per quintam huius sicut est peripheria BED ad lineam A, sic sit diameter BD ad lineam CF; eritque per [S:9] octavam huius, sicut diameter BD ad diametrum CF, sic peripheria BED ad peripheriam CGF; eandem igitur rationem cum habeat peripheria BFD ad peripheriam CGF. quam ad lineam A: aequalis erit, per nonam quinti, lineae A peripheria CGF. Rursum ergo liquet propositum.

Ex quibus manifestum est, et datum circulum alicui rectilineo esse aequalem: itemque dati circuli peripheriam alicui rectae lineae esse aequalem.

Similiter haec enim ostenduntur, mutato tantum supposito: ut scilicet pro superficie circulus, et pro data linea circuli peripheria dari supponatur.

Vocat Maurolicus coni-colurum segmentum coni, abscissum a plano parallelo basi coni, comprehensumque inter duo praedicta plana.

Inizio della pagina
 ->