PROPOSITIO XXII.

Si in portione contenta a recta, et a sectione rectanguli coni trigonum inscribatur basim habens eandem cum portione, et altitudinem eamdem: inscribantur autem, et alia trigona in relictas portiones eandem basim habentia portionibus, et altitudinem eandem utriuslibet trigonorum inscriptorum in relictas portiones: octuplum est trigonum, quod in tota portione inscriptum est.

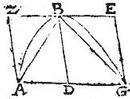
Sit portio ABG qualis dicta est, et secetur recta AG bifariam in D, et ducatur penes diametrum, vel ipsa diameter ad peripheriam recta DB, eritque per 19. huius, portionis ABG vertex signum B; describatur itaque triangulum ABG, eritque ipsius trianguli cum portione, altitudo una, et basis una. Item secetur bifariam AD apud E, et educatur ad peripheriam penes diametrum EZ, quae ipsam quoque AB bifariam secabit [S:193] per 2. sexti, secet apud T, eritque per 19. huius, punctum Z vertex portionis AZB; describatur triangulum AZB, eritque trigoni cum portione AZB, altitudo una, et basis una; non aliter secta bifariam DG apud K, ductaque penes diametrum KH, describatur triangulum BHG; quod cum portione BHG eamdem celsitudinem, eandemque basim habebit. Aio itaque trigonum ABG trigoni AZB, sive trigoni BHG octuplum esse. Connectatur enim EB, et quoniam BD ipsius quidem ZE per 20. huius, epitrita est, ipsius vero ET dupla; quando scilicet DA ipsius AE dupla: propterea ZE ipsius ET sesquialtera est; et ideo ET ipsius TZ dupla. Quare per primam sexti, trigonum AET trigoni ATZ duplum, et trigonum ETB trigoni TBZ duplum. Itaque totum ABE trigonum totius AZB trigoni duplum: Sed per primam sexti, trigonum ABD, trigoni ABE duplum: ergo trigonum ABD trigoni AZB quadruplum: adhuc trigonum ABG trigoni ABD duplum: et ideo trigonum ABG trigoni AZB octuplum. Non aliter idem trigonum ABG demonstrabitur ipsius trigoni BHG octuplum: quod est propositum.

COROLLARIUM.

Itaque trigonum ABG quadruplum est trigonorum AZB, BHG.