F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber secundus 8
<- App. -> <- = ->

PROPOSITIO VIII.

Si per centrum gravitatis trianguli linea aequidistans uni laterum, et reliqua secans ducatur; et in triangulo simili linea correlativo lateri aequidistans ad eandem rationem secet latera, ibit per centrum.

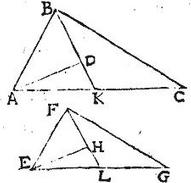
figura 10

Sunto similia triangula ABC, cuius centrum D, et EFG; et per centrum D ipsi AC lateri aequidistans ducatur KDL. In triangulo autem EFG ducatur linea MN aequidistans lateri EG; quod correlativum est lateris AC, et secans latera FE, FG in punctis M, N ad eam rationem, ad quam secantur latera AB, BC in punctis K, L. Aio quod MN it per centrum gravitatis trianguli EFG: nam si linea MN per centrum non it; eat, si possibile est, per centrum linea OP ipsi EG aequidistans, eritque per 6. huius, sicut FO ad OE, sic BK, ad KA: sed per hypothesim, sicut iam BK ad KA, sic FM ad ME: igitur sicut FM ad ME, sic FO ad OE: et coniunctim sicut FE ad EM, sic FE ad EO: quare OE, EM aequales: pars, et totum: quod est absurdum. Omnino igitur MN per centrum trianguli EFG incedit: quod erat demonstrandum.

Inizio della pagina
 ->