F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber secundus 7
<- App. -> <- = ->

PROPOSITIO VII.

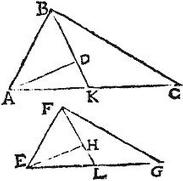
figura 9

Si a relativis angulis similium triangulorum per centra gravitatum rectae agantur: actae ad eamdem rationem secabunt opposita latera.

Sunto similia triangula ABC, cuius centrum D, et EFG, cuius centrum H, et ab angulis aequalibus B, F per centra D, H agantur rectae BDK, FHL coincidentes oppositis lateribus apud K, L puncta: aio quod portiones AK, KC proportionales sunt portionibus EL, LG: coniungantur enim AD, [S:116] EH: eruntque per 7. postulatum, triangula ABD, EFH similia: quandoquidem similium triangulorum ABC, EFG centra sunt D, H: ergo angulus ADB aequalis angulo EHF: et angulus BAD aequalis angulo FEH: itaque supersunt triangula ADK, EHL aequiangula: quamobrem per 4. sexti Euclidis, in triangulis ABC, EFG, sicut AC, ad EG, sic AB ad EF: et in triangulis ABD, EFH, sicut AB ad EF, sic AD ad EH: et in triangulis ADK, EHL sicut AD ad EH, sic AK ad EL. Igitur et sicut AK, ad EL, sic AC ad EG: quapropter per 19. quinti, sicut AC ad EG, sic KC ad LG: et ideo sicut KC ad LG, sic AK ad EL: proportionalia igitur sunt segmenta AKC segmentis ELG: quod est propositum.

Inizio della pagina
 ->