PROPOSITIO IX.
Si ab angulo trianguli cuiuspiam per centrum ad oppositum latus linea ducatur, linea in simili triangulo ducta ab angulo correlativo, et oppositum latus ad eandem rationem secans ibit per centrum.
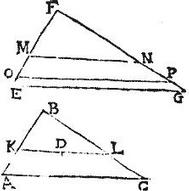
Sunto similia triangula ABC, cuius centrum D, et EFG, et ab angulis correlativis B, F ducantur lineae BK per centrum D: et FL secans latus EG in puncto L ad eam rationem, ad quam secatur latus AC in puncto K. Aio iam quod FL per centrum trianguli EFG incedit: nam si FL per centrum trianguli EFG non incedit; eat per centrum, si possibile est linea FM, eritque per 7. huius, sicut EM ad MG, sic AK ad KC: supponitur autem sicut AK ad KC, sic EL ad LG: ergo sicut EL ad LG, sic EM ad GM, et coniunctim sicut EG, ad GL sic EG, ad GM: quare LG, GM aequales: pars, et totum, quod est impossibile: astruitur ergo propositum.