F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber secundus 24
<- App. -> <- = ->

PROPOSITIO XXIV.

Centrum gravitatis trianguli sic dividit lineam ductam ab angulo ad medium punctum subtensi lateris, ut portio ad angulum recepta dupla sit reliquae.

In triangulo ABC linea a quovis angulo ut B coincidat basi AC in punctum G bifariae sectionis, quae per praecedentem it per centrum trianguli ABC: sit ergo cen[S:127]trum in linea BG in puncto H: demonstrandum est, quod BH dupla est ipsius HG.

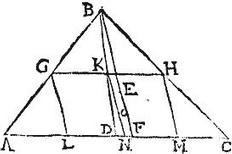
figura 28

Sic, coniungatur CH, et producta coincidat AB lateri apud K punctum: Quae per 21. huius, per aequalia secabit ipsum latus AB apud K, coniugatur KG, quae per 2. sex Euclidis, aequidistabit ipsi BC, et perinde aequiangula, hoc est similia erunt triangula BHC, GHK: itaque ut BC ad KG sic BH ad HG, dupla autem est BC ipsius KG (quandoquidem sicut AB ad AK) ergo et dupla BH ipsius HG: quod est propositum.

Idem aliter: ducatur per H centrum ipsi AC aequidistans linea DE secans latera in punctis D, E: eritque per 13. huius, BD dupla ipsius DA: sed sicut BD ad DA, sic BH ad HG per 2. sex Euclidis; ergo, et BH dupla ipsius HG: quod fuit demonstrandum.

Inizio della pagina
 ->