PROPOSITIO XXV.

Si linea ab angulo quolibet trianguli ad medium punctum subtensi lateris, sic secetur, ut portio ad angulum recepta dupla sit reliquae, punctum sectionis erit centrum gravitatis trianguli.

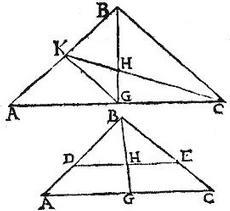
In triangulo ABC ab angulo quolibet B cadat in punctum G linea BG, in quo AC per aequalia dividitur, quae in puncto H ita secetur, ut BH dupla sit ipsius HG: demonstrandum est, quod H punctum est centrum gravitatis trianguli ABC. Omnino enim per 22. vel per 23. praemissas, centrum trianguli ABC est in linea BG, in ea ergo si centrum non est H punctum, sit si possibile est L punctum: eritque percedentem, BL portio dupla ipsius LG: sed per hypothesim BH dupla ipsius HG: igitur tam HG, quam GL fiet tertia pars ipsius BG: et perinde aequales erunt ipsae HG, GL: pars, et totum: quod est impossibile: non est ergo centrum trianguli ABC aliud quam H punctum:

Vel sic (ut in secunda descriptione praecedentis) per punctum H ducatur ipsi AC aequidistans DHE: et quoniam supponitur BH dupla ipsius HG: per 2. sex, et BD dupla ipsius DA: quare per 14. vel 15. huius, DE it per centrum trianguli ABC, sed et BG it per idem centrum per 23. omnino ergo H punctum erit centrum trianguli ABC: quod est propositum.