PROPOSITIO XVII.
Si in quolibet triangulo ducatur linea aequidistans basi, et secans reliqua latera, ita ut portio ad verticem recepta dupla sit reliquae; tunc quae per punctum mediae divisionis ductae unisectorum laterum aequidistat, similiter secat latera, et vicissim per aequalia secatur a ducta.
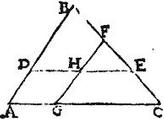
Sit ut prius triangulum ABC, in quo DE aequidistans basi AC secet reliqua latera in punctis D, E, ita ut portiones DB, BE duplae sint portionum AD, EC: et DE per aequalia divisa apud H ducatur FHG aequidistans ipsi AB: aio quod FC, CG portiones duplae sunt reliquarum BF, GA: quodque FG per aequalia secatur apud H: nam cum per hypothesim DH, HE sint aequales : erunt per 2.6. Euclidis, et BF, FE aequales: sed per hypothesim EC dimidium est ipsius BE: aequales ergo sunt BF, FE, EC: et perinde CF dupla ipsius BF, atque CG dupla ipsius GA: itaque per praecedentem., ipsarum DE, FG lateribus trianguli ABC aequidistantium, et latera sic secantium, ut portiones ad angulos duplae sint reliquarum, utraque reliquam per aequalia dividit; et idcirco FG bifariam secatur apud H: quod erat demonstrandum.