F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber secundus 16
<- App. -> <- = ->

PROPOSITIO XVI.

Duarum linearum duobus lateribus cuiuslibet trianguli aequidistantium, et latera reliqua ita secantium, ut portio ad angulum recepta, dupla sit reliquae, utraque alteram per aequalia dividit.

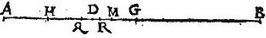
figura 20

In triangulo ABC linea DE aequidistet lateri AC, et linea FG aequidistet lateri AB, quae duae lineae ita secent reliqua latera, ut portiones ad angulos B, C receptae duplae sint reliquarum, hoc est, ut BD ipsius DA, et ideo BE ipsius EC dupla sit: itemque CF ipsius FB, et ideo CG ipsius GA dupla sit, quae lineae secant se invicem in puncto H: aio quod per aequalia se invicem secabunt; hoc est quod ipse DH, HE inter se aequales, et ipsae FH, HG inter se aequales erunt: nam cum per hypothesim, et 2. sexti Euclidis. BE dupla sit ipsius EC: iam tota BC tripla erit ipsius CE: itemque cum CF per eadem dupla sit ipsius FB. Iam tota BC tripla item erit ipsius BF: itaque tam CE quam FB tertia pars est totius BC, et perinde FE tertia pars residua eiusdem: aequale ergo sunt CE, EF, FB lineae: et ideo per 2. sexti Euclidis. in triangulo DBE ipsae DH, HE aequales inter se; et in triangulo GFC ipsae FH, HG similiter aequales inter se erunt; cum aequidistans basi ad eamdem rationem secet latera reliqua: et hoc fuerat demonstrandum.

Inizio della pagina
 ->