PROPOSITIO XV.
Quod praecedens proposuit aliter ostendere.
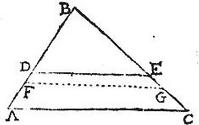
In triangulo ABC latus quodvis ut pote AB secetur apud D; ita ut dupla sit portio BD ipsius DA: aio quod ducta linea per punctum D aequidistans basi AC incedit per centrum trianguli ABC: secentur enim latera singula trianguli ABC per medium in punctis E, F, G: quae coniungantur ductis lineis: sic triangulum ABC sectum erit in quatuor triangula sibi similia, et inter se aequilatera, et aequalia: et quoniam AG est dimidium ipsius AB: atque AD tertia pars eiusdem AB, per hypothesim: idcirco erit DG sexta totius AB, hoc est tertia pars ipsius AG: secetur AD per aequalia in puncto H: erunt AH, HD, DG aequales: harum uni ponatur aequalis tam GK, quam FL: sic enim latus trianguli magni AB in puncto D, et latera triangulorum partialium AG, GB, FE in punctis H, K, L ad eandem rationem secantur: quamobrem si aequidistans basi AC ducta per punctum D, it per centrum trianguli magni: aequidistans ducta per punctum H ibit per centrum trianguli AGE, et per centrum trianguli EFC per 8. huius, et per centrum commune ipsorum per x. Item aequidistans ducta per punctum K ibit per centrum trianguli GBF per 8. Sicut autem est aggregatum ex triangulis AGE, EFC tanquam una pars ad triangulum GBF tanquam alteram partem, sic est spatium KD ad spatium DH, utraque enim ratio dupla: igitur cum aequidistantes per puncta H, K ductae eant per centra partium: aequidistans ducta per punctum D ibit, per 5. huius, per centrum totius, hoc est per centrum commune trium triangulorum AGE, EFC, GBF; sed talis aequidistans per punctum D it per punctum L (quandoquidem aequales, et aequidistantes sunt DG, LF) ergo per 8. it per centrum trianguli FEG: itaque centrum commune trium triangulorum AGE, EFC, GBF tanquam unius partis, et centrum trianguli FEG tanquam alterius partis sunt in aequidistante ducta per punctum D. Quare per 6. praecedentis libri, centrum totius, hoc est trianguli magni ABC erit in eadem aequidistante, sicut iam suppositum est. Convenit itaque ratio centrorum hypothesi. Quod si secus supponatur, absurditas sequetur: sit enim, si possibile est, centrum trianguli ABC in aequidistante per aliud, quam per punctum D ducta, ut pote in aequidistante per punctum M, et ponantur ipsius DM spatii dimidia ipsa spatia HN, KO, LP, DQ, sic enim latus trianguli magni AB in puncto M, et latera triangulorum partialium AG, GB, FE in punctis N, O, P, rursus ad eandem rationem secabuntur, quandoquidem dimidiis adiecta sunt dimidia eius, quod duplo est adiectum: item secetur per aequalia DM in puncto R, eritque OR aequalis ipsi KD, atque RN aequalis ipsi DH, cumque dupla sit KD ipsius DH, et ipsa OR dupla erit ipsius RN, quapropter per ea, quae prius adducta sunt, quoniam centrum trianguli ABC ponitur in aequidistante ipsi AC ducta per punctum M: erit iam centrum commune triangulorum AGE, EFC in aequidistante ducta per punctum N: centrum trianguli GBF in aequidistante ducta per punctum O: centrum porro commune trium triangulorum AGE, EFC, GBF in aequidistante ducta per punctum R, tanquam unius partis; centrum denique trianguli FEG tamquam alte[S:122]rius partis in aequidistante ducta per puncta P, Q: fuit vero centrum totius hoc est trianguli magni ABC in aequidistante ducta per punctum M: itaque aequidistans ducta per centrum totius non est media intra aequidistantes ductas per centra partium. Quod est impossibile per 5. huius. Centrum igitur trianguli ABC non est in alia aequidistante quam per D punctum ducta. Quemadmodum proponitur demonstrandum.
ALIA BREVIS DEMONSTRATIO.
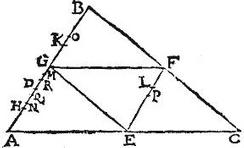
Ex triangulo ABC, praecedentis propositionis, capiatur latus AB, et similiter secetur, ut dictum est: et per punctum D ducatur parallelus basi AC: ostendam rursus quod talis parallelus it per centrum trianguli ABC: nam diviso triangulo ABC in quatuor triangula aequalia, et similia, quorum tria angularia similem situm habent: medium vero conversam positionem; item per ultimum, et penultimum postulatum, et per 27. primi. Centrum commune trium triangulorum angularium erit in parallelo per punctum D, et centrum trianguli medii in eodem parallelo: congruitque ratio ponderum supposito, neque aliter se habere centra possibile est: nam si centrum totalis trianguli sit in parallelo per punctum M, tunc centrum trium triangulorum angularium erit in parallelo per punctum R, ita ut DR spatium sit dimidium spatii DM per ultimum postulatum. Centrum autem trianguli mediani in parallelo per punctum Q per tantumdem spatium DQ ad partes diversas recedente propter contrariam trianguli mediani positionem: unde centrum commune totalis trianguli scilicet, non interiacebit centris partium: quod est absurdum: superest ergo propositum.