PROPOSITIO XIV.
Si in quolibet triangulo linea basi aequidistans ita secet reliqua latera, ut portio ad verticem recepta dupla sit reliquae: secans it per centrum gravitatis trianguli.
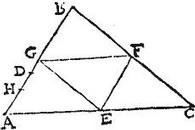
In triangulo ABC ducatur basi AC aequidistans linea DE, ita secans latera, ut BD portio dupla sit ipsius DA: aio quod DE incedit per centrum trianguli ABC: nam si DE per centrum non it, eat si possibile est per centrum ipsa FG aequidistans ipsi AC: eritque per praecedentem, BF dupla ipsius FA: est autem per hypothesim BD dupla ipsius DA: igitur FA tertia pars est totius AB, et DA tertia pars eiusdem: et perinde aequales sunt DA, AF: pars et totum: quod est impossibile: omnino igitur DE per centrum it trianguli ABC.
Alia demonstratio (in figura sequentis propositionis:) ex triangulo ABC sumo latus AB, quod secetur per aqua apud G, et AG linea in tria aequalia GD, DH, HA: et per punctum D ducatur linea parallelus basi AC: aio quod talis parallelus it per centrum trianguli ABC: secto enim triangulo ABC in duo triangula similia, et aequalia super basim AC relicto parallelogrammo: erit centrum parallelogrammi in parallelo per punctum G: centrum autem commune triangulorum ad basim in parallelo per H per 3.2. et per ultimum postulatum: itaque congruit ratio ponderum supposito: quandoquidem centra partium aequalium aequaliter hinc inde distant a centro communi totius: nam duo triangula partialia componunt simul aequum parallelogrammo, et spatia sunt HD, DG, et centrum totius trianguli in linea per punctum D, neque aliter se habere centra possibile est. Sit enim si possibile est centrum totalis trianguli in parallelo per punctum M versus partes B per spatium DM recedens; et tunc per ultimum postulatum, centrum commune triangulorum partialium ad basim secedet eodem versus per spatium HN, quod sit dimidium ipsius DM, quando latus trianguli partialis dimidium est lateris trianguli totalis, correlativa comparando: maior ergo fiet linea MN, quam linea MG: igitur centrum commune partium aequalium non aequaliter distabit a centris partium: quod est absurdum: astruitur ergo propositum.
COROLLARIUM.
Ex his duabus sequitur ut trium linearum per centrum gravitatis trianguli cuiuslibet ductarum, et lateribus singulis aequidistantium unaquaeque, ita secet reliqua latera, ut portio ad angulum recepta dupla sit reliquae, et vicissim, si unaquaeque trium linearum singulis lateribus cuiuslibet trianguli aequidistantium, ita secet reliqua latera, ut portio ad angulum recepta dupla sit reliquae: tunc tres huiusmodi lineae se invicem super centro gravitatis trianguli secabunt.