PROPOSITIO XIII.

Si per centrum gravitatis cuiuslibet trianguli ducatur linea aequidistans basi, et secans reliqua latera; portio lateris ad verticem, recepta erit ad reliquam dupla.

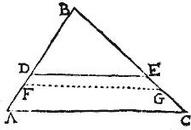
In triangulo ABC ducatur linea per centrum aequidistans basi AC, et secans reliqua latera, ut pote latus AB apud D punctum: aio quod BD portio dupla est ipsius DA: nam per praecedentem, BD maior erit, quam DA: secetur ergo AB per aequalia in puncto G, cadetque punctum D in linea AG: secentur item latera BC, CA per aequalia in punctis E, F, et coniungantur EF, FG, GE: eruntque facta triangula inter se aequilatera, et aequalia: secetur itaque AD per aequalia in puncto H, eritque sicut BA ad AG, sic iam DA ad AH: utraque enim dupla ad utramque, et permutatim, sicut BA ad AD, sic GA ad AH; et disiunctim, sicut BD ad DA, sic GH ad HA: itaque cum aequidistans basi AC ducta per centrum trianguli ABC, secet latus AB apud punctum D: iam per 8. huius, linea ducta per punctum H aequidistans correlativae basi AE, ibit per centrum trianguli AGE, et ideo per centrum trianguli EFC, et per centrum commune triangulorum AGE, EFC per x. huius, sed per 3. huius, centrum parallelogrammi BGEF est in diametro GF aequidistante ipsi AEC: trium igitur aequidistantium euntium per puncta D, G, H, quae per punctum D it per centrum totius trianguli scilicet ABC: quae autem per puncta G, H eunt per centra partium, hoc est, quae per punctum H, it per centrum commune triangulorum AGE, EFC tanquam unius partis: quae autem per punctum G it per centrum parallelogrammi BGEF alterius partis: suntque partes ipsae aequales: aequale est enim parallelogrammum BGEF triangulis AGE, EFC simul sumptis: igitur per corollarium quinti huius, segmenta GD, DH aequidistantibus intercepta sunt aequalia: aequales autem fuerunt DH, HA: aequales ergo sunt GD, DH, HA, et perinde GH dupla ad HA, fuitque sicut GH ad HA, sic BD ad DA; et BD igitur dupla ipsius DA: quod erat demonstrandum.