F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber secundus 12
<- App. -> <- = ->

PROPOSITIO XII.

Si per centrum gravitatis trianguli cuiuslibet basi aequidistans ducatur secans reliqua latera, portio lateris ad verticem trianguli recepta maior erit quam reliqua.

In triangulo ABC agatur basi AC aequidistans per centrum trianguli, et reliqua latera AB, BC secans linea DE: aio quod portio BD maior est portione DA: [S:119]

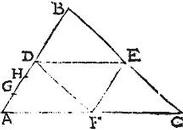
figura 15

nam si BD non sit maior quam DA, erit aut ei aequalis, aut ea minor: si aequalis, tunc per praecedentem centrum trianguli ABC erit intra quadrilaterum ADEC: quod est contrarium supposito, supponitur enim centrum in linea DE. Si autem BD sit minor, quam DA, tunc eo magis centrum trianguli ABC erit intra relictum trapetium ADEC: quod rursum adversatur hypothesi: non est ergo BD aequalis ipsi DA, neque minor ea: maior ergo erit: sicut proponitur demonstrandum.

Inizio della pagina
 ->