PROPOSITIO VIII.

Data solidi conoidis portione plano super axem recto abscissa, sive data sphaeroidis portione, quae minime maior, quam dimidium existat: possibile est ipsi figuram quamdam inscribi, et aliam circumscribi ex cylindris aequalis altitudinis confectam, ita ut circumscripta figura excedat inscriptam excessu, qui sit quocumque dato solido minus.

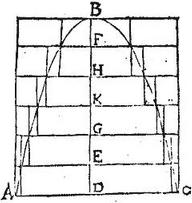
Esto solidi conoidis, sive parabolici, sive hyperbolici, sive sphaeroidis non maioris dimidio portio: quam describit sectio conica, sive parabole, sive hyperbole, sive ellipsis dimidia non maior circa axem BD: item completo quadrilatero rectangulo ABC, quod extra sectionem cadit, atque circa eundem axim revoluto, cylindrus construatur ABC, cuius axis BD secetur in partes aequales: et in totidem cylindros; (aequales enim sunt cylindri portiones per 13. duodecimi) donec una portionum cylindri sit minor dato solido; quae portio habeat axem DE: inde per puncta divisionum axis BD agantur plana aequidistantia ipsi basi cylindricae AC, hoc est recta ad axem BD; quae plana solidum conoides secantia facient circulos per decimam septimam praecedentis libri. Itaque circulo AC sit aequalis circulus quidam in plano aequidistanti per E; qui duo circuli erunt bases portionis cylindricae praedictae cuius axis ED; circulo autem supremo, qui per F aequalis sit circulus quidam in plano supremo per B, qui duo circuli erunt bases cylindri, cuius axis BF: itaque cylindrus cuius axis DE erit maximus, cylindrus vero cuius axis BF minimus cylindrorum componentium figuram circumscriptam solido conoidi: caeteri autem cylindricam figuram componentes fient ascribendo unicuique circulorum in conoide solido per plana caetera factorum circulum aequalem in plano superiori, et exteriorem solido: porro si circulis mediis supponantur circuli aequales singuli singulis in planis inferioribus, et intra solidum cadentes; constituentur ex binis cylindri singuli componentes figuram inscriptam solido, qui cylindri erunt uno pauciores cylindris componentibus figuram circumscriptam. Denique cum cylindrus inscriptus circa axem DE sit aequalis cylindro circumscripto circa axem EG; et inscriptus circa axem EG aequalis circumscripto circum axem GK; et inscriptus circum axem GK sit aequalis circumscripto circa axem KH, et inscriptus circum axem KH aequalis circumscripto circa axem HF. Ac demum inscriptus circum axem HF aequalis circumscripto circa axem FB. Iam manifestum est figuram ex cylindris circumscriptis [S:252] compositam, hoc est figuram circumscriptam solido conoidi, maiorem esse figura ex cylindris inscriptis composita; hoc est ipsa figura eidem solido inscripta in cylindro, cuius axis DE, basis vero circulus radio DA descriptus; sed talis cylindrus minor fuit dato solido. Itaque figura solido conoidi ABC circumscripta supererat figuram eidem solido inscriptam excessu cylindri AEC, qui dato solido minor est. Et hoc possibile fore diximus.